New Toy!

I got excited(!) late last night sketching up a trig problem that deals with rotating circles. I thought that I could maybe whip up a demo in GeoGebra today, to help me learn the geometry software better. --So, tada! :) What are the maximum / minimum lengths of the red spring as the circles rotate at the given rates?

(Or, for those of you too lazy to load the page, here's the pertinent info about this problem.)

Circle A has a radius of 8, and circle C has a radius of 7. The two circles are lined up vertically, and the shortest distance between them, EF, is 5 units. At time t = 0, the points B and D are placed maximally far apart on the circles. As time progresses, Point B rotates about A counterclockwise with the speed of 5 seconds per revolution, and Point D rotates about C with a speed of 6 seconds per revolution. As you can see, a red spring is tied between B and D. Sometimes it stretches, and other times it compresses...

Here is a screenshot (but the visualization demo I made is much more interesting, because it actually rotates...). To create the java applet (or a similar one) yourself in GeoGebra, you would have to do some simple trig involving sine, cosine, period, and scaling/translation, in order to specify the location of the points as a function of t. (Might not be a bad exercise for your kids to animate something like this themselves!) I originally created everything on a coordinate plane, and then in the end I hid all of the coordinate info, so that kids working on this problem would have to do a little more work piecing it together themselves.


Anyway, I started to brainstorm what questions I could ask, and in the end, I was pretty happy with Question C (see the bottom of my linked-to HTML page above), because it can be answered so many ways, as simply as thinking about the fact that one circle has a period of 5 seconds, and the other has a period of 6 seconds, so their LCM of 30 seconds must be the common period. You can also verify this visually by toggling the t value in the GeoGebra applet. :) And, graphically, it looks beautiful! (I had to try a few different number combos, I admit, before I settled upon these final radii and periods.)

This is what it looks like if you graph the length of the red spring over time. With a wee bit of graphing-calc proficiency, you can use a graph like this to verify the period = 30 secs and to find the local max and min, which represent the longest and shortest lengths of the spring, respectively. (Click to open enlarged graph in a different window.)


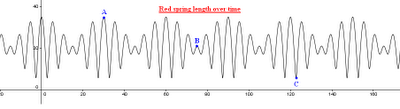
I think you can also lead a rich discussion about what's going on with the two circles using this graph. (What's happening with the circles at points A, B, and C? Why are there parts of the graph where the oscillations are sharp, versus other parts where the oscillations are comparatively minimal? WHY does the oscillation graph show symmetry at t = 15, t = 45, t = 75... even though the two circles are both rotating counterclockwise?) --The best part? The kids can then verify/refute their hypotheses visually by toggling on the t values and comparing what they see in the visualization applet with the data from the graph. Try it! You may be surprised by what you see happening with the circles at t = 15, t = 45, t = 75... (I know I sure was!) :)

...I heart math!

Some variations of this problem I may try to cook up later-later (hopefully in GSP next time): What happens if the circles overlap? What if you have three circles, each controlling one vertex of a triangle? (Or as a computer activity for students: How can you animate a circle that has a specified location, a given radius, and a specific rate of motion?)