I love my 7th-graders! Today was the second time I've played games with them on a Friday afternoon, and they absolutely go nuts for it every time.
One concern I always have during a group game is that only the kids who are up for their turn are engaged. Today I improved that by letting TWO kids from each team go up together, and they can only collaborate AFTER they have both tried the problem independently. When they ring the bell, both people should already have written down the answer on their paper, and I'll randomly call on one of them to EXPLAIN their answer. (So, they had to confer before ringing the bell, and the stronger student was always eagerly explaining to the weaker student how to do it.)
The problems built up in difficulty, so I'd always make sure all students from the class understood the explanations to the previous question before starting another round. Students at their desks were also practicing because they didn't want to be the person to hold their partner up when it's their turn. Overall, the rotations went twice as fast, and everyone was constantly engaged.
By the end of the 80-minute period, even my weakest students were getting through the problems by themselves, and EVERYONE WAS SO EXCITED TO EXPLAIN THEIR ANSWERS! It was great!!
Grab the file here. This one was on filling in missing numbers into linear patterns, and some of it involved integers and decimals. The kids were brilliant! (We also had two exchange students from China playing with us. It was COOL; one of them explained to me in Chinese, and I translated for her in real time for the class, and high-fived her after that round! It was sweet.)
Friday, September 30, 2011
Sunday, September 25, 2011
Numerous Connections to Quadratic Functions
I think that as secondary math teachers, we ought to be aware of as many ways as possible to model quadratic patterns, so we can seamlessly integrate those techniques into our curricula. It's the first non-straight forward pattern that our kids encounter, and it seems to trouble them throughout their secondary careers. Thankfully, there are ties to quadratic modeling from MANY different topics!
To discuss this concretely, let's first have a look at a quadratic pattern:
(2, 7), (3, 9), (4, 12), (5, 16)
In this discussion, I am going to assume that you've already taught kids how to recognize that this is a quadratic pattern, since that discussion should absolutely precede any quadratic skills, methinks!
Neat, eh? I think it's pretty amazing how you can approach a simple quadratic pattern from so many different algebraic methods, and I am a true believer that the more of these integrated approaches we take, the better kids will understand each individual method and be able to transfer their knowledge.
By the way, an 8th-grader came up to me and made an insightful observation, the day following our quick class discussion about why we need 3 points in order to find a path of trajectory (quadratic function) using Dan Meyer's basketball pictures. She asked me, "We need 3 points to find a quadratic function, but we need at least 4 points to verify that the pattern IS quadratic, right?" and she drew me a table on the board with some first and second differences. Brilliant! Yes - 3 points is enough to find an equation, but that's like saying two points form a line. That's the minimal amount of info needed to get the equation, but as soon as you have redundant data points, you will know if your regression form is actually correct! How astute of her to make that observation!
To discuss this concretely, let's first have a look at a quadratic pattern:
(2, 7), (3, 9), (4, 12), (5, 16)
In this discussion, I am going to assume that you've already taught kids how to recognize that this is a quadratic pattern, since that discussion should absolutely precede any quadratic skills, methinks!
Method #1: Helping kids understand at a middle-school level that we find missing coefficients inside equations by plugging in given x's and y's.
For example, given our points above, y = ax^2 + bx + c becomes:
7 = 4a + 2b + c
9 = 9a + 3b + c
12 = 16a + 4b + c
This we can solve in MIDDLE SCHOOL using systems of equations/elimination method.Method #2: When kids get into high school and they start learning about matrices, we can set the same system up as a problem of 3-by-3 matrix, and help them use the calculator to solve it:
(It's a good time to make sure everyone understands why we're using inverse matrices, and what identity means in math, etc.)Method #3: Of course, now that they're in the realm of graphing calculators, we should also teach them how to use quadratic regression to get the values of the coefficients. Method #4: There is another sneakier way of finding the equation using pure quadratics algebra. It's called the Legrange Method, and I learned it this summer at PCMI.
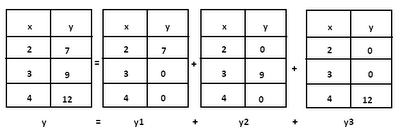
You split the function into smaller, easier quadratic functions by splitting the table and hiding two points at a time:
With a bit of simple algebra, you can figure out that
y1 = 3.5(x - 3)(x - 4)
y2 = -9(x - 2)(x - 4)
y3 = 6(x - 2)(x - 3)
Then, when you simplify each and combine them, you'd get your equation for y! This way is not the easiest, but it does reinforce the idea of roots, plugging in numbers to solve for parts of equation, and expansion/simplification of binomials.Method #5: Individual elements within a quadratic sequence are created as a summation of arithmetic/linear steps! For example, if you look at the example we have here: (2, 7), (3, 9), (4, 12), (5, 16)
f(2) = 7
f(3) = 7 + 2
f(4) = 7 + 2 + 3
f(5) = 7 + 2 + 3 + 4
Inductively,
f(x) = 7 + { 2 + 3 + 4 + ... +(x-1) }
Or, if we use an arithmetic series formula to represent the sum-of-steps:
f(x) = 7 + [2 + (x-1)][(x-2)/2]
Since my arithmetic series has first term = 2, last term = (x-1), and altogether (x-2)/2 pairs of elements.Method #6: There is a name for this trick, but I forget what it is. If we draw out the quadratic sequence as dots, we get:
Here I used the gray dots to represent the initial value.
If you double the added dots at each stage (see blue/black dots below), it now becomes instantly easier to find the pattern, because the length and the width of the resulting rectangle is a simple linear progression in terms of x:
f(x) = initial value + half of rectangular area
f(x) = 7 + 0.5(length times width of rectangle)
f(x) = 7 + 0.5(x + 1)(x - 2)
Neat, eh? I think it's pretty amazing how you can approach a simple quadratic pattern from so many different algebraic methods, and I am a true believer that the more of these integrated approaches we take, the better kids will understand each individual method and be able to transfer their knowledge.
By the way, an 8th-grader came up to me and made an insightful observation, the day following our quick class discussion about why we need 3 points in order to find a path of trajectory (quadratic function) using Dan Meyer's basketball pictures. She asked me, "We need 3 points to find a quadratic function, but we need at least 4 points to verify that the pattern IS quadratic, right?" and she drew me a table on the board with some first and second differences. Brilliant! Yes - 3 points is enough to find an equation, but that's like saying two points form a line. That's the minimal amount of info needed to get the equation, but as soon as you have redundant data points, you will know if your regression form is actually correct! How astute of her to make that observation!
Friday, September 23, 2011
Planned Time to Discuss Math
Today, I am happy because one of my real-life colleagues offered to sit down with me once a week to talk about math. I like the way she put it: "You are good at some things, and I am good at some different things. We can ask each other questions!"
I've never had a setup like this before! I can just talk about whatever I want to talk about, related to math and teaching, with someone else who is years more experienced than me!! We're not really planning partners, so it's not like we're bogged down by needing to discuss X number of lessons or Y issues each week, either.
This, my friends, is going to be sweet!
I've never had a setup like this before! I can just talk about whatever I want to talk about, related to math and teaching, with someone else who is years more experienced than me!! We're not really planning partners, so it's not like we're bogged down by needing to discuss X number of lessons or Y issues each week, either.
This, my friends, is going to be sweet!
Thursday, September 22, 2011
A Fun Pattern
I wanted to share a fun little pattern of the day. This is an extension of other visual patterns we've worked on, but this one right now stomps my 8th-graders, and it's kind of fun to see them stomped. Only about one or two kids have managed to figure out the second equation. A girl asked me if she can model the irregular shape by chopping it up into two regular rectangles, finding each quadratic equation separately, and then recombining them. YES! That's brilliant.

Questions to ask your students:
1. Can you conjecture what the next two stages will look like?
2. Which pattern is linear and which is quadratic? Which geometric property likely affects the type of function that the pattern will have?
3. For each pattern, find an equation that helps you predict the size (number of blocks) in stage x.
4. Can you figure out how many blocks will be in stage 50 of each pattern?
5. Can you figure out when (in which stage) there will be exactly _____ blocks?
Let expansion and factorization fall out as a matter of necessity. I think that's how we can help kids really sink their teeth into those skills, even before we get to "real world" problems.

Questions to ask your students:
1. Can you conjecture what the next two stages will look like?
2. Which pattern is linear and which is quadratic? Which geometric property likely affects the type of function that the pattern will have?
3. For each pattern, find an equation that helps you predict the size (number of blocks) in stage x.
4. Can you figure out how many blocks will be in stage 50 of each pattern?
5. Can you figure out when (in which stage) there will be exactly _____ blocks?
Let expansion and factorization fall out as a matter of necessity. I think that's how we can help kids really sink their teeth into those skills, even before we get to "real world" problems.
Wednesday, September 21, 2011
Progression of Middle School Skills
Teaching so many grades at once has made me re-think (because I have to!) the sequence of topics that we teach in school. This is a work in progress, but here is a rough list of topics in sequence, and what I personally think is ABSOLUTELY NECESSARY for the kids to understand regarding each topic:
* We absolutely need to introduce the idea of linear patterns as soon as possible. Something like:
_____, ______, 3, _______, _______, ________, 47, ________
The kids should be able to do this starting in early 7th grade (or before), well before they even consider what x's and y's are. They should be able to reason it out like this: "In 4 steps, the value goes up 44, so in each step, how much does it go up by??"
This proportional/linear reasoning underlies so much algebra but can be introduced completely without!! (And notice that you can use it to reinforce integer operations and also fractional understanding.)
_______, 0, ______, _______, 1, _______, _______, _______
* Instead of grade 7 being a re-teach of grade 6 skills, we need to focus on estimation skills in grade 7. Can kids plot points on a graph when scale is 3 or bigger?? Can kids plot points on a graph when they have mixed number types? Can kids mentally estimate 5% and 20% and 15% and 90% QUICKLY because they understand how to benchmark against 10%? Can kids figure out which 2 integers 23/9 falls between, AND which of those integers it is closer to??
Estimation needs to be the focus in Grade 7, to help kids see the "bigger picture" of values and less of the rote algorithms.
* Work in Grade 7 on helping kids set up equations. Help them figure out that "x" is the quantity that's being asked. Help them list out all the givens. Help them figure out that most equations are written like "part + part + part = TOTAL" or "part * part = TOTAL" so that they can always try to look for the total in a question. Help them figure out that "each" and "every" represent rates, which represent multiplications somewhere.
* Let kids figure out how to go backwards to find a Mystery Number. Don't try to teach rote algebra. Instead, draw arrow diagrams that represent the steps of evaluation, and kids'll figure out on their own how to work backwards.
* When kids are flying through easy equation setups, give them a twist. Make them figure out that if two quantities add to 20, then they are x and 20-x. Help them figure out why it's not x and x-20. Help them figure out that if two quantities multiply to be 70, then they are x and 70/x, not x and x/70. Because they'll need that flexible understanding down the road.
* Then, proportions. Can kids figure out WHICH situations are proportions and which are NOT?! How about proportions in the coordinate plane - what do they tell us? What about part-to-part ratios vs. part-to-whole ratios?
It sounds silly, but making tables works wonders in reinforcing proportional relationships. Kids will naturally observe that proportional quantities always start at (0, 0) and grow "proportionately" (in lack of another word), and they'll want to develop "shortcuts" like figuring out the scale factor immediately.
* Introduce bivariate linear patterns and introduce non-linearity alongside it. Before we teach any algebra, help kids learn that: x is the cause and y is the effect. Almost ALWAYS. For goodness' sake, don't tell them which variable is x and which is y, and DON'T always put the x on the left side of the table. Let them figure it out.
* Visually introduce linear patterns. Let them play with the idea of building equations and then making predictions, forwards and backwards, with the simple equation. Emphasize the utter importance of thinking about what X and Y each represents in the problem, in order to figure out where to plug in the given starting values. They'll need this understanding down the road in higher algebra, to keep track of the meaning of their computed results.
* Tie slope to UNIT rates. Yes, rise is a rate. But rise/run gives us the UNIT rate, which is more useful more often. Let them graph while THINKING about the meaning of unit rate and initial value. Don't feed them graphing algorithms!
* Then, introduce quadratic patterns and the idea of second differences. DON'T introduce quadratic skills before kids learn to visually recognize quadratic patterns from a table!!
* Help kids learn to find quadratic equations. Even if it's not the easiest way. (I do the Legrange Method and I think my kids hate me for it. Down the road I'll teach them to solve for a, b, c, using a system of equations.)
* Now, can the kid make predictions with a quadratic equation? Forwards and BACKWARDS. Don't let them start on factoring until they see the value of going backwards. If you need to, give them a graphing calculator for now, and tell them that soon we're going to figure out how to "not cheat" with the calculator and how to do that backwards solving-for-x by hand.
* Factor with the box method, and MAKE SURE THAT KIDS UNDERSTAND WHY factoring helps us solve the problem. (Here, insert joke about product of hair counts at NY Yankee Stadium being 0. Why?? It only takes 1 bald man. Start referring to your "zeroed factor" as a bald person.) Then introduce geometric problems that force kids to set up quadratic equations with x's on both sides, to solve them, and then to eliminate nonsensible solutions. The whole shebang. Focus on the idea that not all algebraic solutions always make sense.
* Embed linearity and quadratics in visuals, applications, word problems. Take your time. Make sure kids can viscerally connect to the idea of a slope being a rate and a y-intercept being an initial value; make them go backwards from equations to filling in blanks in a story. Make sure kids graph EVERYTHING and they understand always how the graph and table and equation are all interchangeable.
* Secretly introduce the idea of linear systems through applications like a savings race. Help kids approach the idea of break-even points from a graphical perspective, and use visual puzzles to get them thinking about equivalent quantities and substitution. Finally, wrap it up in a neat algebra bow by tying those methods to traditional algebra symbols and operations.
Make sure your kids can explain how to properly check a system!
* Get back to quadratics and now ask the kids to find quadratic equations fitting tables, using a systems of equations approach. Integrate different concepts into one seamless application for them. Don't let them walk away from this unit not knowing how to find a quadratic equation given ANY quadratic table. Re-emphasize now why we need exactly 3 points to find a quadratic equation. Use Dan Meyer's basketball pictures to let it sink in.
* Introduce square roots and combining square roots through Tangrams and other composite shapes made of right triangles. Tie this into combining like terms in general, and get them to think about decomposing shapes into smaller parts...
* Make sure kids understand dimensions. THEN introduce scaling in the coordinate plane.
* Lastly, exponents. I don't have good ideas for reinforcing exponent rules, except making kids write out all the terms being multiplied. Do you??
I feel like in the end, I'm still missing some topics, but I would be VERY HAPPY if every middle schooler I have the pleasure of teaching can leave with all of these concepts integrated together under their mathematical belt. That'd give us so much to build off of in high school, when the algebra gets trickier. What is your list of middle school must-knows??
* We absolutely need to introduce the idea of linear patterns as soon as possible. Something like:
_____, ______, 3, _______, _______, ________, 47, ________
The kids should be able to do this starting in early 7th grade (or before), well before they even consider what x's and y's are. They should be able to reason it out like this: "In 4 steps, the value goes up 44, so in each step, how much does it go up by??"
This proportional/linear reasoning underlies so much algebra but can be introduced completely without!! (And notice that you can use it to reinforce integer operations and also fractional understanding.)
_______, 0, ______, _______, 1, _______, _______, _______
* Instead of grade 7 being a re-teach of grade 6 skills, we need to focus on estimation skills in grade 7. Can kids plot points on a graph when scale is 3 or bigger?? Can kids plot points on a graph when they have mixed number types? Can kids mentally estimate 5% and 20% and 15% and 90% QUICKLY because they understand how to benchmark against 10%? Can kids figure out which 2 integers 23/9 falls between, AND which of those integers it is closer to??
Estimation needs to be the focus in Grade 7, to help kids see the "bigger picture" of values and less of the rote algorithms.
* Work in Grade 7 on helping kids set up equations. Help them figure out that "x" is the quantity that's being asked. Help them list out all the givens. Help them figure out that most equations are written like "part + part + part = TOTAL" or "part * part = TOTAL" so that they can always try to look for the total in a question. Help them figure out that "each" and "every" represent rates, which represent multiplications somewhere.
* Let kids figure out how to go backwards to find a Mystery Number. Don't try to teach rote algebra. Instead, draw arrow diagrams that represent the steps of evaluation, and kids'll figure out on their own how to work backwards.
* When kids are flying through easy equation setups, give them a twist. Make them figure out that if two quantities add to 20, then they are x and 20-x. Help them figure out why it's not x and x-20. Help them figure out that if two quantities multiply to be 70, then they are x and 70/x, not x and x/70. Because they'll need that flexible understanding down the road.
* Then, proportions. Can kids figure out WHICH situations are proportions and which are NOT?! How about proportions in the coordinate plane - what do they tell us? What about part-to-part ratios vs. part-to-whole ratios?
It sounds silly, but making tables works wonders in reinforcing proportional relationships. Kids will naturally observe that proportional quantities always start at (0, 0) and grow "proportionately" (in lack of another word), and they'll want to develop "shortcuts" like figuring out the scale factor immediately.
* Introduce bivariate linear patterns and introduce non-linearity alongside it. Before we teach any algebra, help kids learn that: x is the cause and y is the effect. Almost ALWAYS. For goodness' sake, don't tell them which variable is x and which is y, and DON'T always put the x on the left side of the table. Let them figure it out.
* Visually introduce linear patterns. Let them play with the idea of building equations and then making predictions, forwards and backwards, with the simple equation. Emphasize the utter importance of thinking about what X and Y each represents in the problem, in order to figure out where to plug in the given starting values. They'll need this understanding down the road in higher algebra, to keep track of the meaning of their computed results.
* Tie slope to UNIT rates. Yes, rise is a rate. But rise/run gives us the UNIT rate, which is more useful more often. Let them graph while THINKING about the meaning of unit rate and initial value. Don't feed them graphing algorithms!
* Then, introduce quadratic patterns and the idea of second differences. DON'T introduce quadratic skills before kids learn to visually recognize quadratic patterns from a table!!
* Help kids learn to find quadratic equations. Even if it's not the easiest way. (I do the Legrange Method and I think my kids hate me for it. Down the road I'll teach them to solve for a, b, c, using a system of equations.)
* Now, can the kid make predictions with a quadratic equation? Forwards and BACKWARDS. Don't let them start on factoring until they see the value of going backwards. If you need to, give them a graphing calculator for now, and tell them that soon we're going to figure out how to "not cheat" with the calculator and how to do that backwards solving-for-x by hand.
* Factor with the box method, and MAKE SURE THAT KIDS UNDERSTAND WHY factoring helps us solve the problem. (Here, insert joke about product of hair counts at NY Yankee Stadium being 0. Why?? It only takes 1 bald man. Start referring to your "zeroed factor" as a bald person.) Then introduce geometric problems that force kids to set up quadratic equations with x's on both sides, to solve them, and then to eliminate nonsensible solutions. The whole shebang. Focus on the idea that not all algebraic solutions always make sense.
* Embed linearity and quadratics in visuals, applications, word problems. Take your time. Make sure kids can viscerally connect to the idea of a slope being a rate and a y-intercept being an initial value; make them go backwards from equations to filling in blanks in a story. Make sure kids graph EVERYTHING and they understand always how the graph and table and equation are all interchangeable.
* Secretly introduce the idea of linear systems through applications like a savings race. Help kids approach the idea of break-even points from a graphical perspective, and use visual puzzles to get them thinking about equivalent quantities and substitution. Finally, wrap it up in a neat algebra bow by tying those methods to traditional algebra symbols and operations.
Make sure your kids can explain how to properly check a system!
* Get back to quadratics and now ask the kids to find quadratic equations fitting tables, using a systems of equations approach. Integrate different concepts into one seamless application for them. Don't let them walk away from this unit not knowing how to find a quadratic equation given ANY quadratic table. Re-emphasize now why we need exactly 3 points to find a quadratic equation. Use Dan Meyer's basketball pictures to let it sink in.
* Introduce square roots and combining square roots through Tangrams and other composite shapes made of right triangles. Tie this into combining like terms in general, and get them to think about decomposing shapes into smaller parts...
* Make sure kids understand dimensions. THEN introduce scaling in the coordinate plane.
* Lastly, exponents. I don't have good ideas for reinforcing exponent rules, except making kids write out all the terms being multiplied. Do you??
I feel like in the end, I'm still missing some topics, but I would be VERY HAPPY if every middle schooler I have the pleasure of teaching can leave with all of these concepts integrated together under their mathematical belt. That'd give us so much to build off of in high school, when the algebra gets trickier. What is your list of middle school must-knows??
Saturday, September 17, 2011
MYP and Grading
I realized when I started teaching in the IB system that a lot of changes were going to have to take place, but what I hadn't realized was that my grading scheme would involuntarily shift towards the mode of Standards-Based Grading.
My understanding is that in MYP (Middle Year Programme, which runs from 6th through 10th grade), students are graded based on four assessment criteria: Knowledge and Understanding (out of 8 points), Communication in Mathematics (out of 6 points), Reflections in Mathematics (out of 6 points), and Mathematical Modeling (out of 8 points). A sort of weighted average of all four criteria of assessment results in their final grade in the class, which is out of 7 possible points.
One clear advantage of this system is that it makes it very clear for these MYP students, which of the four categories they need to focus on and improve. (Hence, I say it's more SBG-style.)
What is very interesting to me is that a typical quiz that I give may only cover two assessment criteria (Knowledge and Understanding, and Communication in Mathematics). I look at their overall performance on the quiz, and if they understood just over half of the material, for example, I would assign a 5 out of 8. I also look at the amount of work shown, plus the one or two explanation questions, and assign a Communications in Mathematics grade out of a total of 6 points. (If a kid shows a lot of appropriate work throughout the quiz but fails to complete the explanation question, for example, I see that as a 3 out of 6.) This means that a kid could have missed some concepts on the quiz, but if they are really good about explaining what they did and showing every step of the work, they are earning credit toward a different assessment criterion. This I like, because it shows an emphasis toward the process used, as well as the final result.
As from last year, I continue to offer opportunities for students to revise their graded work and to re-submit for points. This year, I'm even more generous - they can revise even their project writeups, since my classes are smaller and I can handle the extra grading/feedback workload. And my new perspective is that the quiz process is truly three parts: 1. pre-quiz practice (ie. practice quizzes, done in class), 2. the quiz itself, returned with copious written feedback but not a score, 3. the kid revises the quiz, comes to explain every question to me. I used to think that the last step was optional, but this year my opinions on that have changed, under the new MYP grading system. Under the new grading system, I expect my MYP kids to do this revision step, and it counts towards their "Reflections in Mathematics" grade (as well as bumps up their original quiz score). I think of Reflections in Mathematics as a grade I am assigning towards meta-cognition in mathematics, if you will. I will take a similar approach with projects that are returned, by asking kids to take a close look at a rubric and to pick out specific things they need to work on the next time in order to show improved mastery.
Another thing that I am trying is to introduce formal structure for mathematical lab writeup as soon as possible. I don't quite think my seventh graders are ready for it yet, but by 8th and 9th grade, the students should be doing at LEAST 2 or 3 formal lab writeups a year, complete with intro, plan, data analysis and prediction, and final error analysis. This is because at the end of Grade 11, as part of their IB curriculum, they are supposed to do an "internal assessment" of this form, and I think if we leave it until 11th grade for the teacher to tackle this idea of a formal writeup in math, that is way too late.
So, to that end, I took the formal Grade 11 lab writeup rubric from the IB program and I modified it into a more kid-friendly language for use with younger students. You are welcome to take a look! The first trial run of this lab writeup I am doing is with the cup-stacking activity from Dan Meyer. My (low) Grade 9 group has been working on the rough draft of this writeup in class so that they can ask me for help. Some of them were pretty disorganized and had already lost their data from before, so I let them re-measure the data and explain the steps to me to ensure that they understand what they're doing. It's a very worthwhile process, and I think that forcing them to do this lab writeup has truly enhanced every kid's understanding of the activity. Even from my English language-learners in class, I have seen much more understanding be articulated than I could have hoped for, even within the rough drafts. It's great!
Here are some files that might be useful, if you're thinking about doing this kind of thing: lab writeup checklist and the modeling rubric. They are works in progress, but I figured they're a good starting point.
My understanding is that in MYP (Middle Year Programme, which runs from 6th through 10th grade), students are graded based on four assessment criteria: Knowledge and Understanding (out of 8 points), Communication in Mathematics (out of 6 points), Reflections in Mathematics (out of 6 points), and Mathematical Modeling (out of 8 points). A sort of weighted average of all four criteria of assessment results in their final grade in the class, which is out of 7 possible points.
One clear advantage of this system is that it makes it very clear for these MYP students, which of the four categories they need to focus on and improve. (Hence, I say it's more SBG-style.)
What is very interesting to me is that a typical quiz that I give may only cover two assessment criteria (Knowledge and Understanding, and Communication in Mathematics). I look at their overall performance on the quiz, and if they understood just over half of the material, for example, I would assign a 5 out of 8. I also look at the amount of work shown, plus the one or two explanation questions, and assign a Communications in Mathematics grade out of a total of 6 points. (If a kid shows a lot of appropriate work throughout the quiz but fails to complete the explanation question, for example, I see that as a 3 out of 6.) This means that a kid could have missed some concepts on the quiz, but if they are really good about explaining what they did and showing every step of the work, they are earning credit toward a different assessment criterion. This I like, because it shows an emphasis toward the process used, as well as the final result.
As from last year, I continue to offer opportunities for students to revise their graded work and to re-submit for points. This year, I'm even more generous - they can revise even their project writeups, since my classes are smaller and I can handle the extra grading/feedback workload. And my new perspective is that the quiz process is truly three parts: 1. pre-quiz practice (ie. practice quizzes, done in class), 2. the quiz itself, returned with copious written feedback but not a score, 3. the kid revises the quiz, comes to explain every question to me. I used to think that the last step was optional, but this year my opinions on that have changed, under the new MYP grading system. Under the new grading system, I expect my MYP kids to do this revision step, and it counts towards their "Reflections in Mathematics" grade (as well as bumps up their original quiz score). I think of Reflections in Mathematics as a grade I am assigning towards meta-cognition in mathematics, if you will. I will take a similar approach with projects that are returned, by asking kids to take a close look at a rubric and to pick out specific things they need to work on the next time in order to show improved mastery.
Another thing that I am trying is to introduce formal structure for mathematical lab writeup as soon as possible. I don't quite think my seventh graders are ready for it yet, but by 8th and 9th grade, the students should be doing at LEAST 2 or 3 formal lab writeups a year, complete with intro, plan, data analysis and prediction, and final error analysis. This is because at the end of Grade 11, as part of their IB curriculum, they are supposed to do an "internal assessment" of this form, and I think if we leave it until 11th grade for the teacher to tackle this idea of a formal writeup in math, that is way too late.
So, to that end, I took the formal Grade 11 lab writeup rubric from the IB program and I modified it into a more kid-friendly language for use with younger students. You are welcome to take a look! The first trial run of this lab writeup I am doing is with the cup-stacking activity from Dan Meyer. My (low) Grade 9 group has been working on the rough draft of this writeup in class so that they can ask me for help. Some of them were pretty disorganized and had already lost their data from before, so I let them re-measure the data and explain the steps to me to ensure that they understand what they're doing. It's a very worthwhile process, and I think that forcing them to do this lab writeup has truly enhanced every kid's understanding of the activity. Even from my English language-learners in class, I have seen much more understanding be articulated than I could have hoped for, even within the rough drafts. It's great!
Here are some files that might be useful, if you're thinking about doing this kind of thing: lab writeup checklist and the modeling rubric. They are works in progress, but I figured they're a good starting point.
Friday, September 16, 2011
Connect the dots
I am introducing my 7th-graders to graphing points, in anticipation of the upcoming discussions about algebraic/graphical linearity and similarity ratios.
To this end, I went ahead and enhanced an assignment I have already used in the past. They're going to do Connect the Dots individually on one picture I've designed, and then make big posters in groups on other designs while still practicing plotting points! (I'm very excited about this. I need some wall decorations very soon, and I think these posters are going to be perfect.)
I've come up with three designs besides the original individual one. The kids are not going to be told what the designs are until they graph them out. The feedback for me (and for them) is instantaneous, because I can visually see when their picture doesn't look quite right. We haven't done this yet, but I think doing it on the gridded chart paper has an added benefit of forcing them to use scales bigger than 1 (since there are fewer grids on the big paper) -- which will in turn force them to consider how to graph points that are not neatly on or halfway between two labels on the axis. Go approximation!
Doing it on big poster also will have other benefits, methinks: 1. encouraging group work (they will be encouraged to divide up the points to work in parallel), 2. extra neatness (using pencils to plot points and rulers to outline before outlining with markers).
Here are the files, in case you want to adopt this activity: Design #1 (individual work, in notebook) and #2 (group work/poster) and Design #3 and #4 (group work/poster).
I'm pretty excited. I'll even take pictures this time of their final products!!
To this end, I went ahead and enhanced an assignment I have already used in the past. They're going to do Connect the Dots individually on one picture I've designed, and then make big posters in groups on other designs while still practicing plotting points! (I'm very excited about this. I need some wall decorations very soon, and I think these posters are going to be perfect.)
I've come up with three designs besides the original individual one. The kids are not going to be told what the designs are until they graph them out. The feedback for me (and for them) is instantaneous, because I can visually see when their picture doesn't look quite right. We haven't done this yet, but I think doing it on the gridded chart paper has an added benefit of forcing them to use scales bigger than 1 (since there are fewer grids on the big paper) -- which will in turn force them to consider how to graph points that are not neatly on or halfway between two labels on the axis. Go approximation!
Doing it on big poster also will have other benefits, methinks: 1. encouraging group work (they will be encouraged to divide up the points to work in parallel), 2. extra neatness (using pencils to plot points and rulers to outline before outlining with markers).
Here are the files, in case you want to adopt this activity: Design #1 (individual work, in notebook) and #2 (group work/poster) and Design #3 and #4 (group work/poster).
I'm pretty excited. I'll even take pictures this time of their final products!!
Saturday, September 10, 2011
Binders and Other German Updates
Did you know that in Germany, binders (for holding papers) only have two rings, not three? That's a Geometry postulate in action! How many points does it take to secure the hinge of a piece of paper?



(There is at least one advantage to doing the two-hole punch; your hole-puncher is smaller, and has a retractable frame that comes out to meet the full length of the paper.)

In other news, another interesting tidbit about Germany: If your baby is half German or more, you can only name them certain "acceptable German names" from a list. Yikes.
Also, liver is very popular here; something like a traditional fare. You have to be careful, because German words are long and if a word ends in leber it means it's some type of chunky liver dish.
I've started discussing current events weekly with my home room, just to gauge how they feel about certain things (and maybe in the long run, I can gently influence their opinions on some issues). We started yesterday with talking about how well over 500 cars have been set on fire in the city of Berlin this year, by arsonists, and why they think this is happening. Interesting stuff, because I don't think that adults have the answers to this question...



(There is at least one advantage to doing the two-hole punch; your hole-puncher is smaller, and has a retractable frame that comes out to meet the full length of the paper.)

In other news, another interesting tidbit about Germany: If your baby is half German or more, you can only name them certain "acceptable German names" from a list. Yikes.
Also, liver is very popular here; something like a traditional fare. You have to be careful, because German words are long and if a word ends in leber it means it's some type of chunky liver dish.
I've started discussing current events weekly with my home room, just to gauge how they feel about certain things (and maybe in the long run, I can gently influence their opinions on some issues). We started yesterday with talking about how well over 500 cars have been set on fire in the city of Berlin this year, by arsonists, and why they think this is happening. Interesting stuff, because I don't think that adults have the answers to this question...
Friday, September 9, 2011
Week in Review
This week was a busy one in teaching. In hindsight, I am feeling very upbeat about how classes are going, even though as a new teacher in the system I still feel a certain amount of self-doubt daily.
It's getting better. I have kids coming up to me and saying that they think the class is going very well for them; I am at least one to two weeks ahead in planning lessons; so far the kids have done very well on their first quizzes; and I feel like kids are learning a good amount of relevant mathematics in spite of the IB "pressure."
Things are also going very well with my colleagues as well. I have not yet asked people to observe me on specific classroom skills, but this year I've had an unprecedented amount of people inside my room because they're there to provide push-in support to specific kids with learning or language issues. For the first time ever, I have language specialists looking over my quizzes and providing me with a revised copy of simpler language for my ELL kids! Amazing!
And, I am excited about getting around to some project-y type things. :) First up is next week, when we will be building tetrahedral kites in Grade 8 and modeling the pattern using a quadratic equation. --I can't wait!!
Another thing on the (distant) horizon is the possibility of going away on a math team trip in February. My colleague said that there are good networking possibilities this way, and I can meet a lot of great European "maths" teachers who are very experienced in the IB curriculum. That sounds fabulous...
Anyway, enough blabbage. You can grab my weekly lessons here. Save the link; I'll keep replacing it with new lessons each week, so that if you are a math teacher and want some resources, you can always grab at my latest lessons at any time.
It's getting better. I have kids coming up to me and saying that they think the class is going very well for them; I am at least one to two weeks ahead in planning lessons; so far the kids have done very well on their first quizzes; and I feel like kids are learning a good amount of relevant mathematics in spite of the IB "pressure."
Things are also going very well with my colleagues as well. I have not yet asked people to observe me on specific classroom skills, but this year I've had an unprecedented amount of people inside my room because they're there to provide push-in support to specific kids with learning or language issues. For the first time ever, I have language specialists looking over my quizzes and providing me with a revised copy of simpler language for my ELL kids! Amazing!
And, I am excited about getting around to some project-y type things. :) First up is next week, when we will be building tetrahedral kites in Grade 8 and modeling the pattern using a quadratic equation. --I can't wait!!
Another thing on the (distant) horizon is the possibility of going away on a math team trip in February. My colleague said that there are good networking possibilities this way, and I can meet a lot of great European "maths" teachers who are very experienced in the IB curriculum. That sounds fabulous...
Anyway, enough blabbage. You can grab my weekly lessons here. Save the link; I'll keep replacing it with new lessons each week, so that if you are a math teacher and want some resources, you can always grab at my latest lessons at any time.
Wednesday, September 7, 2011
Combining Classes
I ran Dan Meyer's cup stacking activity today with a group of combined classes -- mine (9th-grade low group) and my colleague Tania's (9th-grade high group). It was my colleague's suggestion and I thought it was an interesting experiment, so we went ahead and ran with it.
The plan was that we would combine our classes, I'd run the activity, and then afterwards she would give me feedback on how she observed it went and how she thinks it could be changed for next time. She will then do the activity with her other class (I believe it's a 10th-grade low group) on her own.
Anyway, we did it! It was very interesting. I am glad we did it, but I don't know if it's something I would want to do regularly. Here are some quick thoughts:
* Discipline was challenging (although it still went OK). The high-level kids were a lot brattier than I had anticipated; they didn't bother listening to any suggestions I made during whole-class discussions, and they went ahead and made up their own methods anyway, and ran up to me during class to try to tell me how much better their method was.
* I noticed that my "low" group was really trying to keep up with the other guys, so it was good motivation for them. I didn't get a chance, however, to circulate and make sure that they were each individually understanding every part of the assignment as I normally do, since the higher level kids were working fast and they were always ready to move on to the next step.
* In the end, one group made a very accurate prediction (83 cups, right on the money). Others were off by quite a bit (most were in the high 70s range). It was a good check of their over-confidence, I think. (3 minutes into the assignment and everyone was already ready to tell me how many cups they thought we needed.) We started to have a really good discussion of sources of error, but then...
* Apparently today was Picture Day. So, near the end of our discussion, over 2/3 of the kids left with their homeroom teacher for pictures. Oops, I guess it's bad planning on my part.
* Finally, I think the kids are not really understanding the value of mathematical process. They seemed to only want to know if their initial guess is correct. I think maybe we can address this by running this lesson a bit differently. We can first test out their predictions to show them concretely that they are wrong, and then choose a different person (of different height) to use as our new target of modeling.
* In the end, when I opened it up for questions, one kid asked why we decided to combine the high-low classes. I think that speaks to the school culture; the kids (and their families) are overly focused on who's in what level class, and not on whether they're doing quality mathematics.
* Afterwards, Tania thought the whole thing was really great! She said that in the future iterations, the only thing she would change is to project in the background the stage of modeling we're in (planning, data collection, modeling, prediction, testing, error analysis), so that kids can be more clued in throughout the process, to the bigger picture. Great suggestion! Me gusta. :)
Have you tried something like this sort of combined classes at your school? If not, maybe give it a whirl and let me know what you think.
The plan was that we would combine our classes, I'd run the activity, and then afterwards she would give me feedback on how she observed it went and how she thinks it could be changed for next time. She will then do the activity with her other class (I believe it's a 10th-grade low group) on her own.
Anyway, we did it! It was very interesting. I am glad we did it, but I don't know if it's something I would want to do regularly. Here are some quick thoughts:
* Discipline was challenging (although it still went OK). The high-level kids were a lot brattier than I had anticipated; they didn't bother listening to any suggestions I made during whole-class discussions, and they went ahead and made up their own methods anyway, and ran up to me during class to try to tell me how much better their method was.
* I noticed that my "low" group was really trying to keep up with the other guys, so it was good motivation for them. I didn't get a chance, however, to circulate and make sure that they were each individually understanding every part of the assignment as I normally do, since the higher level kids were working fast and they were always ready to move on to the next step.
* In the end, one group made a very accurate prediction (83 cups, right on the money). Others were off by quite a bit (most were in the high 70s range). It was a good check of their over-confidence, I think. (3 minutes into the assignment and everyone was already ready to tell me how many cups they thought we needed.) We started to have a really good discussion of sources of error, but then...
* Apparently today was Picture Day. So, near the end of our discussion, over 2/3 of the kids left with their homeroom teacher for pictures. Oops, I guess it's bad planning on my part.
* Finally, I think the kids are not really understanding the value of mathematical process. They seemed to only want to know if their initial guess is correct. I think maybe we can address this by running this lesson a bit differently. We can first test out their predictions to show them concretely that they are wrong, and then choose a different person (of different height) to use as our new target of modeling.
* In the end, when I opened it up for questions, one kid asked why we decided to combine the high-low classes. I think that speaks to the school culture; the kids (and their families) are overly focused on who's in what level class, and not on whether they're doing quality mathematics.
* Afterwards, Tania thought the whole thing was really great! She said that in the future iterations, the only thing she would change is to project in the background the stage of modeling we're in (planning, data collection, modeling, prediction, testing, error analysis), so that kids can be more clued in throughout the process, to the bigger picture. Great suggestion! Me gusta. :)
Have you tried something like this sort of combined classes at your school? If not, maybe give it a whirl and let me know what you think.
Tuesday, September 6, 2011
Linking Linear Functions and Quadratic Functions
In hopes of reconciling the big gap that often seems to divide linear and quadratic algebra, I used a variation of this activity today and it worked out well. I gave the kids a linear pattern, followed by a square of that pattern, and the kids had to make the connection and figure out that their linear function now transformed into a quadratic one. Then I tagged on some extra dots in a third pattern and they had to figure out that the third pattern now had extra constants.
We used today's activity as a segue into how to expand/simplify quadratic expressions, and they were so excited! (These 8th-graders saw some pieces of quadratic skills last year, but they were happy to be introduced to the box method of multiplication today.)
I made this file (as linked above) to be a follow-up activity to use during a future class, to reinforce the connections they've already made today. After that, I think I'll be ready to go into how to find quadratic equations from a table of values!!
PS. In the interest of less scaffolding, I'm going to hand this sheet to the kids with only the last problem showing. If they can do it, they should try to do it without looking at the problems before; otherwise they can move through the scaffolded "hints" and return to that problem...
PPS. The earlier activity I used is here. I think it's nice to start with a square relationship because the kids can immediately visualize that it will end up looking "quadratic"...
We used today's activity as a segue into how to expand/simplify quadratic expressions, and they were so excited! (These 8th-graders saw some pieces of quadratic skills last year, but they were happy to be introduced to the box method of multiplication today.)
I made this file (as linked above) to be a follow-up activity to use during a future class, to reinforce the connections they've already made today. After that, I think I'll be ready to go into how to find quadratic equations from a table of values!!
PS. In the interest of less scaffolding, I'm going to hand this sheet to the kids with only the last problem showing. If they can do it, they should try to do it without looking at the problems before; otherwise they can move through the scaffolded "hints" and return to that problem...
PPS. The earlier activity I used is here. I think it's nice to start with a square relationship because the kids can immediately visualize that it will end up looking "quadratic"...
Monday, September 5, 2011
A different approach to linear equations?
I've been experimenting with something and I think it might be working! So, here it is. I am going to describe briefly how I approach linear reasoning with my 7th-graders and then open it up for feedback.
1. I draw a visual pattern with dots.

2. I guide the kids to look for how many dots are added at each stage.
3. The kids visually group dots into n groups of k, where n matches the stage # and k matches the stepwise increase. They'll notice that at each stage, there is a certain number of "leftover" dots.

4. Kids start to generate expressions like 1(3) + 1 to represent "1 group of 3, plus 1 extra dot." Then 2(3) + 1 for the next stage, then 3(3) + 1 for the next stage...

5. Eventually, kids can figure out that for stage 1000, the number of dots involved would be 1000(3) + 1. (This inductive thinking, it turns out, takes a couple of days to develop and for them to feel comfortable with...)
6. You then coax them into figuring out that for any stage n, the formula is n(3) + 1. It helps to keep pointing in turn at the formula and back at the concrete numerical examples 1(3) + 1, 2(3) + 1, etc. to emphasize that n is just a placeholder.
7. When kids start to gain confidence in their formula, ask them to start making predictions for small stages n=5 or n=6 and then verify their results by actually continuing the visual patterns.
8. After doing this a bunch of times, they then try to do this with numbers instead of visual dots.
The goal is that they should be able to look at a rough "table" that looks like this (with no actual dots drawn):
Stage 1: 16 dots
Stage 2: 20 dots
Stage 3: 24 dots
...and figure out that the algebraic expression for predicting the size at stage n is n(4) + 12, and then also understand that that formula matches 1(4) + 12, 2(4) + 12, 3(4) + 12, etc... One advantage I have already noticed about this method of teaching linear formulas is that it continuously reinforces the idea that the formula is merely an abstraction (or generalization) of an already-existing pattern.
9. Then, when they're comfortable with the entire process, repeat with negative slopes. Instead of circling groups of added dots, they start circling spaces of taken away dots.


A kid should be able to look at this (after a bit of guidance) and write the equation y = 16 - x(2) for dots at stage x.
What do you think? Do you think this is another rote method of linear patterns, or do you think this could actually increase student understanding of linear equations? Where do you think I should go from here, to transition their understanding into a formal knowledge of linear patterns within the coordinate plane?
PS. You are welcome to download all my lessons thus far (and planned ahead a bit, even!) here. Teaching 5 grades at once is super fun!!
1. I draw a visual pattern with dots.

2. I guide the kids to look for how many dots are added at each stage.
3. The kids visually group dots into n groups of k, where n matches the stage # and k matches the stepwise increase. They'll notice that at each stage, there is a certain number of "leftover" dots.

4. Kids start to generate expressions like 1(3) + 1 to represent "1 group of 3, plus 1 extra dot." Then 2(3) + 1 for the next stage, then 3(3) + 1 for the next stage...

5. Eventually, kids can figure out that for stage 1000, the number of dots involved would be 1000(3) + 1. (This inductive thinking, it turns out, takes a couple of days to develop and for them to feel comfortable with...)
6. You then coax them into figuring out that for any stage n, the formula is n(3) + 1. It helps to keep pointing in turn at the formula and back at the concrete numerical examples 1(3) + 1, 2(3) + 1, etc. to emphasize that n is just a placeholder.
7. When kids start to gain confidence in their formula, ask them to start making predictions for small stages n=5 or n=6 and then verify their results by actually continuing the visual patterns.
8. After doing this a bunch of times, they then try to do this with numbers instead of visual dots.
The goal is that they should be able to look at a rough "table" that looks like this (with no actual dots drawn):
Stage 1: 16 dots
Stage 2: 20 dots
Stage 3: 24 dots
...and figure out that the algebraic expression for predicting the size at stage n is n(4) + 12, and then also understand that that formula matches 1(4) + 12, 2(4) + 12, 3(4) + 12, etc... One advantage I have already noticed about this method of teaching linear formulas is that it continuously reinforces the idea that the formula is merely an abstraction (or generalization) of an already-existing pattern.
9. Then, when they're comfortable with the entire process, repeat with negative slopes. Instead of circling groups of added dots, they start circling spaces of taken away dots.


A kid should be able to look at this (after a bit of guidance) and write the equation y = 16 - x(2) for dots at stage x.
What do you think? Do you think this is another rote method of linear patterns, or do you think this could actually increase student understanding of linear equations? Where do you think I should go from here, to transition their understanding into a formal knowledge of linear patterns within the coordinate plane?
PS. You are welcome to download all my lessons thus far (and planned ahead a bit, even!) here. Teaching 5 grades at once is super fun!!
Subscribe to:
Posts (Atom)