Things I am excited about:
* Teaching kids about variables in the 7th grade! My kids are doing a couple of days of looking for Mystery Numbers given things like "You take a mystery number, add 5 to it, then divide by 8, then square what you have, and the final result is 100. What was the mystery number?" and either working backwards or drawing arrow flow diagrams in order to reason backwards in their heads. It has been crazy cool, because they are then able to take an equation written with "??" as the mystery number, and then use the same backwards logic to solve it WITHOUT ANY ROTE TEACHING!!
And all of this, they did without having been introduced to the notion of x!! (The equations transition to using smiley faces. I don't get why we keep asking all kids to use the terrifying "x" upon introduction to variables. Isn't a smiley face much less intimidating?)
Then, the plan is that I'll model some function machine type of predictable behavior until they get sick of me and they can tell me what I should return if they give me a number called "BLAH". Then they do the same exercise in writing until they get really good/comfortable at representing generalizations using simple algebraic symbols. Then we do some cooler visual patterns.
* My realization: Asking kids to make equations from tables is MUCH LESS COOL than giving them an evolving picture and asking them to find an equation that predicts the picture at any stage N in the future. I'm doing this across all grades and the kids can't seem to get enough of it.
* Another (far more experienced) teacher and I are planning for our classes to do Dan Meyer's cup-stacking activity together. I'm really excited, because 1. I've never run an activity before with two classes of kids, half of whom I don't know. 2. I know this activity has worked superbly for me in the past, and it's a perfect opportunity for me to get feedback from another super experienced colleague on how to fine-tune my delivery and questioning and scaffolding.
I'm nervous, but I think it has potential to be glorious!!
Addendum 31/8/11: Here are some links... Mystery Numbers, What are variables, and Visual patterns to algebra.
Monday, August 29, 2011
Saturday, August 27, 2011
Scaffolding
Dan Meyer wrote a nice post about suggested restructuring of a Geometry assignment recently. It got me thinking about how I could guide my students through this involving, but rich, task.
First, if you have not tried the problem yourself (and read through Dan's post on this), you should do it. It's a great problem, I think. At first glance it seems fairly obvious, but upon further examination, it isn't. I'm still not sure if I took the "easiest" approach or not, and I'd be curious if you solved it an entirely different way.
But, solving the problem and creating opportunities for students to solve the problem are two entirely different beasts. I think if I were to use this problem, it could be "taught" in steps by breaking it down as shown below, but it's not clear 1. whether all students (or most students) would understand this problem, and 2. what I hope the students would gain or retain from this problem. I guess the latter bothers me more.
(In the picture below, "All Students" means all students would be encouraged to independently explore/figure out the important relationships. "Teacher guided" is more like places where I would intervene and provide hints.)
How would you present this problem? Would you scaffold more than what I propose above? The idea is that, in my class, I would give kids a few hints, one at a time, and see how many of them can run with it. If they can't, I'd guide them more heavily and hope that I can stop a bit further down the line for them to re-gain independence on the problem. But that's a fine line, because at that point, are they doing the thinking or have I stripped them of that opportunity?
Do you find the process of maintaining a cognitively demanding task challenging? How do you manage it to balance the need to make the task accessible to students (not just upon the entry point, but throughout the task) and still not over-simplifying the cognitively demanding parts for them?
First, if you have not tried the problem yourself (and read through Dan's post on this), you should do it. It's a great problem, I think. At first glance it seems fairly obvious, but upon further examination, it isn't. I'm still not sure if I took the "easiest" approach or not, and I'd be curious if you solved it an entirely different way.
But, solving the problem and creating opportunities for students to solve the problem are two entirely different beasts. I think if I were to use this problem, it could be "taught" in steps by breaking it down as shown below, but it's not clear 1. whether all students (or most students) would understand this problem, and 2. what I hope the students would gain or retain from this problem. I guess the latter bothers me more.
(In the picture below, "All Students" means all students would be encouraged to independently explore/figure out the important relationships. "Teacher guided" is more like places where I would intervene and provide hints.)
How would you present this problem? Would you scaffold more than what I propose above? The idea is that, in my class, I would give kids a few hints, one at a time, and see how many of them can run with it. If they can't, I'd guide them more heavily and hope that I can stop a bit further down the line for them to re-gain independence on the problem. But that's a fine line, because at that point, are they doing the thinking or have I stripped them of that opportunity?
Do you find the process of maintaining a cognitively demanding task challenging? How do you manage it to balance the need to make the task accessible to students (not just upon the entry point, but throughout the task) and still not over-simplifying the cognitively demanding parts for them?
Friday, August 26, 2011
Week 1 Math Lessons
Here are all the worksheets I used this week or plan on using earlyish next week. They're organized by class and roughly labeled by topic. If you use something and have feedback for me to improve, please let me know! More sharing is merrier. There are some Mimi-made homework worksheets within the file "Week 1 activities" because I'm lame and didn't separate it out. They're outlined in the format I talked about before... broken down into student-assessment, optional practice, extension problems, and teacher assessment.
Happy Friday! :)
Happy Friday! :)
Thursday, August 25, 2011
Day 2!
This year has been very interesting so far, and today was only Day 2. Teaching 5 grades at once is a wild experience; in the first 1.5 days I've simultaneously:
(What's been the most challenging about this is that most of this was material I had to create from scratch without previous lesson plans to fall back onto, and I think that's going to be the norm for this year.)
As it turns out, I have two kids who don't speak ANY English, and that's going to be a real challenge/interesting experience this year, I think. I'm going to need to do drastic modification for them, like asking them to bring bilingual dictionaries to class, keeping a vocabulary journal, and I will be pumping all the assignments through a Google translator for them to have two copies, one in English and one in (crappy translation of) their native language. It helps that I will have a push-in language assistant, so I'm going to do everything I can to make sure we work together to help these kids.
Craziness. I'm a bit stressed, you know, as might be expected with the big change. But it's good. Today I had a really productive day with every group, and it felt great. Let's hope tomorrow's a good day! :)
...Did I mention that our school does not have bells? We expect kids to get to class on time based on a culture of respect for the schedule and the class. They've been doing this for about 7 or so years now. It's still early in the year for me, but I think it actually works! Amazing.
* Taught matrix multiplication through application to weighted class averages (Grade 12)
* Reviewed fraction models, comparison of fractions/decimals, and what types of things can be modeled with fractions through stations work (Grade 7)
* Run a paired "blind drawing" activity to teach basic geometry vocabulary -- points, lines, planes, parallel, intersect, collinear, coplanar, etc -- and to practice visualization from words. (Grade 9)
* Started a "Savings Race" algebra task involving comparing/relating multiple representations (Grade 9)
* Used a border-of-square-pool rich task to introduce patterns, generalization through algebra, and re-arrangement of equations (Grade 8)
* Umm, and I haven't even seen my 11th-graders yet!! Tomorrow'll be the first day. On the agenda is looking at a rich patterns task and moving them through it to generate linear functions and to start to look at how to generate quadratic functions from a table of values.
(What's been the most challenging about this is that most of this was material I had to create from scratch without previous lesson plans to fall back onto, and I think that's going to be the norm for this year.)
As it turns out, I have two kids who don't speak ANY English, and that's going to be a real challenge/interesting experience this year, I think. I'm going to need to do drastic modification for them, like asking them to bring bilingual dictionaries to class, keeping a vocabulary journal, and I will be pumping all the assignments through a Google translator for them to have two copies, one in English and one in (crappy translation of) their native language. It helps that I will have a push-in language assistant, so I'm going to do everything I can to make sure we work together to help these kids.
Craziness. I'm a bit stressed, you know, as might be expected with the big change. But it's good. Today I had a really productive day with every group, and it felt great. Let's hope tomorrow's a good day! :)
...Did I mention that our school does not have bells? We expect kids to get to class on time based on a culture of respect for the schedule and the class. They've been doing this for about 7 or so years now. It's still early in the year for me, but I think it actually works! Amazing.
Friday, August 19, 2011
Math Teachers at Play #41
Willkommen! Welcome to the Math Teachers at Play blog carnival! Whether you are a teacher, homeschooler, parent, or a math enthusiast interested in general discussions about mathematics, there is a little bit of something for everyone here. Some of these links came as direct submissions by bloggers, and the others came from my Google Reader.
To start, here are some fun facts about the number 41:
To start, here are some fun facts about the number 41:- Starting with 41, if you add 2, then 4, then 6, then 8, etc... you would get a string of 40 prime numbers in a row!
- 41 is also a Centered Square Number, which means that it is the sum of two consecutive squares -- 42 and 52, in this case. Can you figure out how this picture relates to the Center Square Numbers, and use the picture to explain why all Center Square Numbers are 1 (mod 4)?
- If you substitute 41 into n for the quadratic expression x2 - x + n, then the expression will evaluate to be prime for all integer values of x = 0, 1, 2, ..., n-1. There are only 6 such values for n, and they're called the "Lucky Numbers of Euler." 41 is the greatest of these lucky numbers.
- One molecule of Penicillin G has 41 atoms.
- On very special occasions in the UK (such as when President Obama visited the Buckingham Palace or when a royal birth takes place), a 41-gun salute is used to mark the occasion.
- In their 1996 album Crash, the Dave Matthews Band recorded a song called "#41." It was the most performed song on their tour that summer.
Caffeine Coquette has written a nice commentary on why we should not be praising children for counting well. Even though her piece is intended for an audience educating young children, there are lots of parallels in the higher grades.BASIC ALGEBRA AND GEOMETRY
Tracey Mansted offers a beautiful collection of methods to introduce young students to new math concepts while keeping away from the drill and kill.
Bon Crowder presents some fun ways to incorporate cuisenaire rods into coordinate-plane math and also how to teach math while crossing the street!SECONDARY MATHEMATICS
Sue Downing tells us a fun story about a few kids who know how to ask the right questions when given a bad math problem.
Denise over at Let's Play Math forwarded a post written by one of her students, reflecting on why a0 must equal 1 using exponent rules as justification.
Guillermo P. Bautista, Jr. uses the properties of a tessellated parallelogram to illustrate angle relationships within a single parallelogram.
Alex Washoe (whose blog is about birds) uses some neat examples from nature to illustrate how animals and humans can do complicated mathematics in the blink of an eye based on instincts alone. It's nice to know that pigeons can figure out the Monty Hall problem faster than I can.MISCELLANEOUS
In his series called Engaging Math Activities for the Summer Break, Alexander Bogomolny presents a type of shuffling algorithm and asserts that the algorithm will terminate. Also check out his other activities for ideas on fun ways to introduce new concepts.
John Cook points out that there exists an elegant theorem regarding nonzero terms of a polynomial and the number of distinct roots. He also recommends a short video from Dr. J illustrating some real-world examples of statistics.
In case you haven't already seen this, Kate Nowak presents a good problem that can generate a lot of questions and different approaches. It's a nice rich problem you can keep in the back of your pocket, because it is tied to various concepts but would still work well as a standalone task.
The latest in his Mathematics in the Real World series, David Wees presents a connection between families and math.
Ashli Black writes a brilliant tip on how to use Jeopardy-style slides to drop hints on which mathematical concepts are intimately interconnected. Are your students thinking fast in order to beat you to the punchline of the lesson?
Erlina Ronda presents how to use repeated patterns to introduce the Pascal's Triangle and its connection to counting.
Since I am a sucker for systems of instant feedback, I recommend reading Bowman Dickson's guest post on Sam Shah's page about modeling with integrals in GeoGebra. Bowman has since written a series of guest blog entries, and you should definitely check them out! I met him over the summer at a teacher program; he is an excellent teacher with some fresh ideas.
From my own blog, I am going to plug some resources we developed at the Park City Math Institute over the summer for assessing your implementation of the 8 Mathematical Practices of the Common Core State Standards. Both the rubric and the supplemental document are still just drafts, but I hope that you will find them useful as you think about modifying your instruction in the new school year.
VISIT OUR SISTER CARNIVALS
Gary Antonick presents a fun, interactive puzzle on eliminating equilateral triangles, and links it nicely to the idea of questioning in mathematics.
Terrance Banks shares a few tips on planning for the first days of school. Another place you can look for first-day ideas is over at the MS Math Wiki.
Edmund Harriss shares the specs on how to build a hexayurt dome. If you teach Geometry, you can start by asking your students to create the nets from scratch, using only compasses and straight edges. You might be surprised how difficult it is for kids to figure out spatially where to construct the next polygon in the 2-D net.
Lucas Allen shares his frustration with the media as he reflects on the question, "Are some kids just born bad at math?"
Not to get all commercial-y on you (This post is not sponsored, I promise!), but it looks like Microsoft Mathematics 4.0 is free and has some neat features, such as 3-D graphing.
Carnival of MathematicsFINAL WORDS
Mathematics and Multimedia
Carnevale della Matematica
...And that sums up this issue of Math Teacher at Play! I hope you have enjoyed these articles. The next edition of the carnival will be hosted at Math is Not a Four Letter Word, due to come out on September 16, 2011. Submissions must be relevant to either students or teachers of preK-12 mathematics. Old posts are OK, but due to the large amounts of readers, please do not submit an article if it has already appeared in a previous edition.
Thursday, August 18, 2011
Some Juicy Problems from Exeter Math 3
When I was at Klingenstein Summer Institute, I met a rock star math teacher who showed us a video of her kids working on Exeter problem sets. She just lets them work at their own paces, and when they're done, they decide who's going to go up to the board to put up their solutions, and then they discuss the differences and decide together what the correct answer is. The entire time during the class discussion, she says close to nothing! It was amazing. The level of engagement and self-start from her kids was mesmerizing and very inspirational.
In the real world, we all have our own state-mandated or school-mandated curricula to cover, but I've heard so many good things about this Exeter thing that I decided to try to work through one of the books to see for myself what this Exeter fuss is all about. Then, life got crazy and I didn't have time to do this. So far, I've only done a little over 70 pages of Math 3, even though my original intention was to do all of Math 3 before school starts. And thus far, my impression of the Exeter problem sets is that they feel a lot like the PCMI problem sets. The problems escalate in complexity and connections between skills from the beginning of the book to its end. Within each page, the problems are not all related to the same topic, thereby forcing kids to really think about which older concepts connect to this one. It moves nicely along the spectrum from the concrete to the abstract; it is evident by the sequence of problems that certain concepts the students are expected to develop independently of the teacher's instruction. Other concepts (such as 3-D vector math and relationships between points, lines, planes in 3-D space, or parametrized equations) I feel that the teacher would need to intervene more heavily to bridge the gaps between the pages. Regardless, the problem sets constantly push students to be independent problem-solvers, and each algebra skill is introduced while embedded in deeper connections. Some of the probability problems can also be readily changed to into experiments, which is delightful to me. :)
I also noticed, at least for me, that the problem sets were tediously slow in the beginning, as I tried to rack my brain to figure out which math concepts in my past applied to these situations I had never seen before. 70 pages later, I can skim a page and only stop to do one problem to make sure that I can do it. I am sure your kids would speed up as well, as they move through the pages and begin to connect concepts more effortlessly.
I found it useful along the way to keep track of the juiciest problems, because then regardless of what curricula I teach, I can pull out and adapt those juiciest problems to my own classes. I am not sure how much time I will have in the upcoming weeks to finish up the task I had started, so I'll share what I have right now, hopefully just in time for some of your upcoming math units. If you're Facebook friends with me, the first few problems should look familiar... Exeter owns all the credit for this material, obviously, but they are very generous in sharing their problem sets publicly, so I don't feel so bad about re-posting them here.
Here we go, some of my favorite problems thus far:
There are two circles that go through (9, 2). Each one is tangent to both coordinate axes. Find the center and the radius for each circle. Start by drawing a clear diagram.
----
Find the total grazing area of the goat G represented in the figure (a top view) shown at right. The animal is tied to a corner of a 40' × 40' barn, by an 80' rope. One of the sides of the barn is extended by a fence. Assume that there
is grass everywhere except inside the barn.
----
Point by point, a dilation transforms the circle x2 − 6x + y2 − 8y = −24 onto the circle x2 − 14x + y2 − 4y = −44. Find the center and the magnification factor of this transformation.
(Continuation) The circles have two common external tangent lines, which meet at the dilation center. Find the size of the angle formed by these lines, and write an equation for each line.
----
A coin of radius 1 cm is tossed onto a plane surface that has been tesselated by right triangles whose sides are 8 cm, 15 cm, and 17 cm long. What is the probability that the coin lands within one of the triangles?
----
To win the carnival game Ring Ding, you must toss a wooden ring onto a grid of rectangles so that it lands without touching any of the grid lines. The ring has a 3-inch diameter, the rectangles are twice as long as they are wide, and the game has been designed so that you have a 28% chance of winning. What are the dimensions of each rectangle?
----
Let A = (0, 0, 0), B = (9, 8, 12), and C = (6, 2, 3). Find coordinates for the point on line AB that is closest to C.
----
The diagram below shows a rectangular solid, two of whose vertices are A = (0, 0, 0) and G = (4, 6, 3). Find the point on segment AC that is closest to the midpoint of segment GH.
----
Let A = (−7,−4) and B = (7, 4), and consider the fact that the dot product of vectors PA and PB is zero. Describe the configuration of all points P = (x, y) that fit this requirement.
----
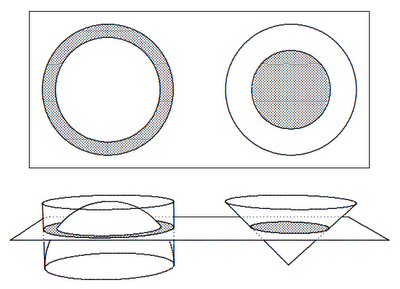A hemisphere of radius 8 is inscribed in a cylinder of radius 8 and height 8. The figure shows top and side views of the hemisphere, the cylinder, and a cone whose radius and height are both 8, and whose base and vertex are coplanar with the bases of the cylinder.
Consider that part of the cylinder that is outside (above) the hemisphere. Slice this region by a plane that is parallel to the cylinder base and 5 inches above the equator of the hemisphere. The intersection is a ring between two concentric circles. The same plane slices the cone, creating a disk. Show that the ring and the disk have the same area.
(Continuation) Suppose now that the three radii and two heights are all r. Show that the ring and the disk have the same area, no matter what the height of the slicing plane.
(Continuation) If the cone were filled with liquid, it could be poured into the cylinder, which still has the hemisphere stuck in the bottom. Will all the liquid fit? Expressed in terms of r, what is the volume of the cone? of the empty cylinder? of the hemisphere?
(Continuation) Show that a sphere of radius r encloses a volume of (4/3)πr3.
----
The rectangle shown has been formed by fitting together four right triangles. As marked, the sizes of two of the angles are α and β (Greek “alpha” and “beta”), and the length of one segment is 1. Find the two unmarked angles whose sizes are α and α + β. By labeling all the segments of the diagram, discover formulas for sin(α+β) and cos(α + β), written in terms of sin α, cosα, sinβ, and cosβ.
----
Imagine covering an unlimited plane surface with a single layer of pennies, arranged so that each penny touches six others tangentially. What percentage of the plane is covered?
----
The table shows the results of a probability experiment. Forty-eight dice were rolled, and each die that showed "2" on top (a deuce) was removed. The remaining dice were rolled again, and deuces were removed. This procedure was repeated until all the dice were gone.
Each entry in the left column is a roll number. The corresponding entry in the right column is the number of dice that had not yet turned up deuces after this roll.
These variables are not linearly related. What happens if you try to apply logarithms to straighten this data?
(Continuation) If forty-eight dice are rolled once, how many do you expect to remain after removing the deuces? How many dice do you expect to remain after two applications of the above procedure? After ten applications?
(Continuation) If a prize were offered for predicting how many rolls will be needed to remove all 48 dice, what would your guess be? Explain.
----
The figure at right shows an outermost 1 × 1 square, within which appears an inscribed circle, within which appears an inscribed square, within which appears another inscribed circle, within which appears another inscribed square. Although the figure does not show it, this process can be continued indefinitely. Let L1 = 1 be the length of a side of the first (largest) square, L2 be the length of a side of the second square, L3 be the length of a side of the third square, and so on. Show that the numbers L1, L2, L3, ... form a geometric sequence, and calculate L20.
(Continuation) Let An be the area of the nth square. Is the sequence A1, A2, A3, ... geometric? Explain.
----
When the note middle C is struck on a piano, it makes a string vibrate at 262 cycles per second. When the corresponding note one octave higher (denoted C') is struck, it makes a string vibrate at 524 cycles per second (twice as fast as the first string). These two numbers form part of a geometric sequence of frequencies
. . ., C, C#, D, D#, E, F, F#, G, G#, A, A#, B, C', . . .
known as equal-tempered tuning. Given C = 262 and C'= 524, find the frequency of G, and the frequency of the note that is n steps above middle C. (For example, F is 5 steps above C.)
(Continuation) Without calculating any of the indicated frequencies, explain why the ratio G:C is the same as the ratio A:D, which is the same as the ratio B:E. Now calculate the ratio G:C and show that it is approximately equal to 3:2, the musical interval known as a fifth. The disagreement between the two ratios is why some violinists do not like to make music with pianists.
----
On the same system of coordinate axes, graph the circle x2 + y2 = 25 and the ellipse 9x2 + 25y2 = 225. Draw the vertical line x = 2, which intersects the circle at two points, called A and B, and which intersects the ellipse at two points, called C and D. Show that the ratio AB :CD of chord lengths is 5:3. Choose a different vertical line and repeat the calculation of the ratio of chord lengths. Finally, using the line x = k (with |k| < 5, of course), find expressions for the chord lengths and show that their ratio is 5:3. Where in the diagram does the ratio 5:3 appear most conspicuously? Because the area enclosed by the circle is known to be 25π, you can now deduce the area enclosed by the ellipse.
(Continuation) What is the area enclosed by the ellipse x2/a2 + y2/b2 = 1?
----
The Hoyts company has a fleet of 1000 cars for one-day local rentals, which must be leased from either the Exeter office or the Hampton office. The company expects that 70 percent of the cars rented in Exeter return to the Exeter office, 60 percent of the cars rented in Hampton return to the Hampton office, and all cars return to one office or the other. Assume that all 1000 cars are rented each day, and that 200 of the rental cars are in Exeter and 800 are in Hampton on Monday morning.
(a) What distribution of cars is expected on Tuesday morning?
(b) What distribution of cars is expected on Wednesday morning?
(Continuation) Verify that the equations
(a) What information do the last two lines convey when n = 1?
(b) The last two lines could be written in matrix form as
.
Verify this. Then find a 2×2 matrix M so that [En Hn ] = [En-1 Hn-1 ]M.
(Continuation)Let v = [200 800] be the initial distribution of cars. Thus vM is the distribution of cars on Tuesday morning.
(a) What does the matrix product (vM)M = vM2 represent?
(b) What does the matrix product vM10 represent?
(c) Matrix M is an example of a transition matrix. After you label its rows and columns, interpret the entries of M as probabilities.
(d)The sum of the entries in each row of M is 1; how is this significant?
(Continuation) Solve the equation [x 1000−x]M = [x 1000−x]. Interpret.
----
The reflection property of parabolas. Let F be the focus of a parabola, and let P be an arbitrary point on the parabola. Let μ be the line through P that is parallel to the axis of symmetry of the parabola; this means that μ intersects the directrix perpendicularly at a point N. Let λ be the perpendicular bisector of FN.
(a) Explain why P is on λ.
(b) Explain why λ is tangent to the parabola.
(c) Explain why λ bisects angle FPN.
(d) Justify the title of this problem.
---
A typical long-playing phonograph record (once known as an LP) plays for about 24 minutes at 33 1/3 revolutions per minute while a needle traces the long groove that spirals slowly in towards the center. The needle starts 5.7 inches from the center and finishes 2.5 inches from the center. Estimate the length of the groove.
----
On 1 July 2011, you deposit 1000 dollars into an account that pays 6 percent interest annually. How much is this investment worth on 1 July 2031? Before you turn your calculator on, write a calculator-ready expression for the answer.
(Continuation) On 1 July 2012, you deposit 1000 dollars into an account that pays 6 percent interest annually. How much is this investment worth on 1 July 2031? Answer the same question for deposits made on 1 July 2012, 1 July 2014, and so forth, until you see a pattern developing in your calculator-ready expressions.
(Continuation) Suppose that you deposit 1000 dollars into the same account on 1 July every year. The problem is now to calculate the combined value of all these deposits on 1 July 2031, including the deposit made on that final day. Rather than getting the answer by tediously adding the results of twenty-one separate (but similar) calculations, we can find a shorter way. Let V stand for the number we seek, and observe that
(Continuation) Any list first, first·multiplier, first·multiplier2, . . . , in which each term is obtained by multiplying its predecessor by a fixed number, is called a geometric sequence. A geometric series, on the other hand, is an addition problem formed by taking consecutive terms from some geometric sequence. Two examples: 16 + 24 + 36 + 54 is a four-term geometric series whose sum is 130, and 32−16+8−4+· · ·+0.125 is a nine-term geometric series whose sum is 21.375. Consider now the typical geometric series, which looks like first + first·multiplier + first·multiplier2 + · · · + last. Find a compact, easy-to-calculate formula for the sum of all these terms.
PS. To save you some googling, you can access the entire Exeter Math 3 text here.
In the real world, we all have our own state-mandated or school-mandated curricula to cover, but I've heard so many good things about this Exeter thing that I decided to try to work through one of the books to see for myself what this Exeter fuss is all about. Then, life got crazy and I didn't have time to do this. So far, I've only done a little over 70 pages of Math 3, even though my original intention was to do all of Math 3 before school starts. And thus far, my impression of the Exeter problem sets is that they feel a lot like the PCMI problem sets. The problems escalate in complexity and connections between skills from the beginning of the book to its end. Within each page, the problems are not all related to the same topic, thereby forcing kids to really think about which older concepts connect to this one. It moves nicely along the spectrum from the concrete to the abstract; it is evident by the sequence of problems that certain concepts the students are expected to develop independently of the teacher's instruction. Other concepts (such as 3-D vector math and relationships between points, lines, planes in 3-D space, or parametrized equations) I feel that the teacher would need to intervene more heavily to bridge the gaps between the pages. Regardless, the problem sets constantly push students to be independent problem-solvers, and each algebra skill is introduced while embedded in deeper connections. Some of the probability problems can also be readily changed to into experiments, which is delightful to me. :)
I also noticed, at least for me, that the problem sets were tediously slow in the beginning, as I tried to rack my brain to figure out which math concepts in my past applied to these situations I had never seen before. 70 pages later, I can skim a page and only stop to do one problem to make sure that I can do it. I am sure your kids would speed up as well, as they move through the pages and begin to connect concepts more effortlessly.
I found it useful along the way to keep track of the juiciest problems, because then regardless of what curricula I teach, I can pull out and adapt those juiciest problems to my own classes. I am not sure how much time I will have in the upcoming weeks to finish up the task I had started, so I'll share what I have right now, hopefully just in time for some of your upcoming math units. If you're Facebook friends with me, the first few problems should look familiar... Exeter owns all the credit for this material, obviously, but they are very generous in sharing their problem sets publicly, so I don't feel so bad about re-posting them here.
Here we go, some of my favorite problems thus far:
There are two circles that go through (9, 2). Each one is tangent to both coordinate axes. Find the center and the radius for each circle. Start by drawing a clear diagram.
----
Find the total grazing area of the goat G represented in the figure (a top view) shown at right. The animal is tied to a corner of a 40' × 40' barn, by an 80' rope. One of the sides of the barn is extended by a fence. Assume that there
is grass everywhere except inside the barn.
----
Point by point, a dilation transforms the circle x2 − 6x + y2 − 8y = −24 onto the circle x2 − 14x + y2 − 4y = −44. Find the center and the magnification factor of this transformation.
(Continuation) The circles have two common external tangent lines, which meet at the dilation center. Find the size of the angle formed by these lines, and write an equation for each line.
----
A coin of radius 1 cm is tossed onto a plane surface that has been tesselated by right triangles whose sides are 8 cm, 15 cm, and 17 cm long. What is the probability that the coin lands within one of the triangles?
----
To win the carnival game Ring Ding, you must toss a wooden ring onto a grid of rectangles so that it lands without touching any of the grid lines. The ring has a 3-inch diameter, the rectangles are twice as long as they are wide, and the game has been designed so that you have a 28% chance of winning. What are the dimensions of each rectangle?
----
Let A = (0, 0, 0), B = (9, 8, 12), and C = (6, 2, 3). Find coordinates for the point on line AB that is closest to C.
----
The diagram below shows a rectangular solid, two of whose vertices are A = (0, 0, 0) and G = (4, 6, 3). Find the point on segment AC that is closest to the midpoint of segment GH.
----
Let A = (−7,−4) and B = (7, 4), and consider the fact that the dot product of vectors PA and PB is zero. Describe the configuration of all points P = (x, y) that fit this requirement.
----
A hemisphere of radius 8 is inscribed in a cylinder of radius 8 and height 8. The figure shows top and side views of the hemisphere, the cylinder, and a cone whose radius and height are both 8, and whose base and vertex are coplanar with the bases of the cylinder.
Consider that part of the cylinder that is outside (above) the hemisphere. Slice this region by a plane that is parallel to the cylinder base and 5 inches above the equator of the hemisphere. The intersection is a ring between two concentric circles. The same plane slices the cone, creating a disk. Show that the ring and the disk have the same area.
(Continuation) Suppose now that the three radii and two heights are all r. Show that the ring and the disk have the same area, no matter what the height of the slicing plane.
(Continuation) If the cone were filled with liquid, it could be poured into the cylinder, which still has the hemisphere stuck in the bottom. Will all the liquid fit? Expressed in terms of r, what is the volume of the cone? of the empty cylinder? of the hemisphere?
(Continuation) Show that a sphere of radius r encloses a volume of (4/3)πr3.
----
The rectangle shown has been formed by fitting together four right triangles. As marked, the sizes of two of the angles are α and β (Greek “alpha” and “beta”), and the length of one segment is 1. Find the two unmarked angles whose sizes are α and α + β. By labeling all the segments of the diagram, discover formulas for sin(α+β) and cos(α + β), written in terms of sin α, cosα, sinβ, and cosβ.
----
Imagine covering an unlimited plane surface with a single layer of pennies, arranged so that each penny touches six others tangentially. What percentage of the plane is covered?
----
The table shows the results of a probability experiment. Forty-eight dice were rolled, and each die that showed "2" on top (a deuce) was removed. The remaining dice were rolled again, and deuces were removed. This procedure was repeated until all the dice were gone.
Each entry in the left column is a roll number. The corresponding entry in the right column is the number of dice that had not yet turned up deuces after this roll.
These variables are not linearly related. What happens if you try to apply logarithms to straighten this data?
(Continuation) If forty-eight dice are rolled once, how many do you expect to remain after removing the deuces? How many dice do you expect to remain after two applications of the above procedure? After ten applications?
(Continuation) If a prize were offered for predicting how many rolls will be needed to remove all 48 dice, what would your guess be? Explain.
----
The figure at right shows an outermost 1 × 1 square, within which appears an inscribed circle, within which appears an inscribed square, within which appears another inscribed circle, within which appears another inscribed square. Although the figure does not show it, this process can be continued indefinitely. Let L1 = 1 be the length of a side of the first (largest) square, L2 be the length of a side of the second square, L3 be the length of a side of the third square, and so on. Show that the numbers L1, L2, L3, ... form a geometric sequence, and calculate L20.
(Continuation) Let An be the area of the nth square. Is the sequence A1, A2, A3, ... geometric? Explain.
----
When the note middle C is struck on a piano, it makes a string vibrate at 262 cycles per second. When the corresponding note one octave higher (denoted C') is struck, it makes a string vibrate at 524 cycles per second (twice as fast as the first string). These two numbers form part of a geometric sequence of frequencies
. . ., C, C#, D, D#, E, F, F#, G, G#, A, A#, B, C', . . .
known as equal-tempered tuning. Given C = 262 and C'= 524, find the frequency of G, and the frequency of the note that is n steps above middle C. (For example, F is 5 steps above C.)
(Continuation) Without calculating any of the indicated frequencies, explain why the ratio G:C is the same as the ratio A:D, which is the same as the ratio B:E. Now calculate the ratio G:C and show that it is approximately equal to 3:2, the musical interval known as a fifth. The disagreement between the two ratios is why some violinists do not like to make music with pianists.
----
On the same system of coordinate axes, graph the circle x2 + y2 = 25 and the ellipse 9x2 + 25y2 = 225. Draw the vertical line x = 2, which intersects the circle at two points, called A and B, and which intersects the ellipse at two points, called C and D. Show that the ratio AB :CD of chord lengths is 5:3. Choose a different vertical line and repeat the calculation of the ratio of chord lengths. Finally, using the line x = k (with |k| < 5, of course), find expressions for the chord lengths and show that their ratio is 5:3. Where in the diagram does the ratio 5:3 appear most conspicuously? Because the area enclosed by the circle is known to be 25π, you can now deduce the area enclosed by the ellipse.
(Continuation) What is the area enclosed by the ellipse x2/a2 + y2/b2 = 1?
----
The Hoyts company has a fleet of 1000 cars for one-day local rentals, which must be leased from either the Exeter office or the Hampton office. The company expects that 70 percent of the cars rented in Exeter return to the Exeter office, 60 percent of the cars rented in Hampton return to the Hampton office, and all cars return to one office or the other. Assume that all 1000 cars are rented each day, and that 200 of the rental cars are in Exeter and 800 are in Hampton on Monday morning.
(a) What distribution of cars is expected on Tuesday morning?
(b) What distribution of cars is expected on Wednesday morning?
(Continuation) Verify that the equations
E0 = 200provide a recursive description of the rental-car distribution.
H0 = 800
En = 0.70En-1 + 0.40Hn-1
Hn = 0.30En-1 + 0.60Hn-1
(a) What information do the last two lines convey when n = 1?
(b) The last two lines could be written in matrix form as
.
Verify this. Then find a 2×2 matrix M so that [En Hn ] = [En-1 Hn-1 ]M.
(Continuation)Let v = [200 800] be the initial distribution of cars. Thus vM is the distribution of cars on Tuesday morning.
(a) What does the matrix product (vM)M = vM2 represent?
(b) What does the matrix product vM10 represent?
(c) Matrix M is an example of a transition matrix. After you label its rows and columns, interpret the entries of M as probabilities.
(d)The sum of the entries in each row of M is 1; how is this significant?
(Continuation) Solve the equation [x 1000−x]M = [x 1000−x]. Interpret.
----
The reflection property of parabolas. Let F be the focus of a parabola, and let P be an arbitrary point on the parabola. Let μ be the line through P that is parallel to the axis of symmetry of the parabola; this means that μ intersects the directrix perpendicularly at a point N. Let λ be the perpendicular bisector of FN.
(a) Explain why P is on λ.
(b) Explain why λ is tangent to the parabola.
(c) Explain why λ bisects angle FPN.
(d) Justify the title of this problem.
---
A typical long-playing phonograph record (once known as an LP) plays for about 24 minutes at 33 1/3 revolutions per minute while a needle traces the long groove that spirals slowly in towards the center. The needle starts 5.7 inches from the center and finishes 2.5 inches from the center. Estimate the length of the groove.
----
On 1 July 2011, you deposit 1000 dollars into an account that pays 6 percent interest annually. How much is this investment worth on 1 July 2031? Before you turn your calculator on, write a calculator-ready expression for the answer.
(Continuation) On 1 July 2012, you deposit 1000 dollars into an account that pays 6 percent interest annually. How much is this investment worth on 1 July 2031? Answer the same question for deposits made on 1 July 2012, 1 July 2014, and so forth, until you see a pattern developing in your calculator-ready expressions.
(Continuation) Suppose that you deposit 1000 dollars into the same account on 1 July every year. The problem is now to calculate the combined value of all these deposits on 1 July 2031, including the deposit made on that final day. Rather than getting the answer by tediously adding the results of twenty-one separate (but similar) calculations, we can find a shorter way. Let V stand for the number we seek, and observe that
V = 1000(1.06)0 + 1000(1.06)1 + · · · + 1000(1.06)19 + 1000(1.06)20is the very calculation that we wish to avoid. Obtain a second equation by multiplying both sides of this equation by 1.06, then find a way of combining the two equations to obtain a compact, easy-to-calculate formula for V .
(Continuation) Any list first, first·multiplier, first·multiplier2, . . . , in which each term is obtained by multiplying its predecessor by a fixed number, is called a geometric sequence. A geometric series, on the other hand, is an addition problem formed by taking consecutive terms from some geometric sequence. Two examples: 16 + 24 + 36 + 54 is a four-term geometric series whose sum is 130, and 32−16+8−4+· · ·+0.125 is a nine-term geometric series whose sum is 21.375. Consider now the typical geometric series, which looks like first + first·multiplier + first·multiplier2 + · · · + last. Find a compact, easy-to-calculate formula for the sum of all these terms.
PS. To save you some googling, you can access the entire Exeter Math 3 text here.
Wednesday, August 10, 2011
Changes for the New Year!
One of the reasons why I love being a teacher is that each school year offers a fresh start -- a chance to do it better. Over the summer, I had an opportunity to listen to a lot of great speakers and to figure out for myself what changes I would like to introduce this year. Some of the things they said were not new; I had heard it all once in grad school, and had even read some of the same articles before. But, back then, I was in my first or second year of teaching and everything was about survival. I did not have the luxury of thinking about how giving a 5-second wait time can make a world of difference in my class. I needed to put out fires and to make sure that kids were doing thoughtful assignments and that the unit was cohesive and that kids were learning good habits from me and that the problems are scaffolded appropriately.
I think that as a slightly less newbie teacher now (I still feel very green, now going into my 6th year), I am at a different place in my career and my PD. I am fortunate to have had some great mentors along the way and some great resources for working on developing lessons that have worked out OK for me and the kids. Now I need to focus on my classroom craft, on how I ask questions, on building a better relationship with kids, on making sure that every kid is thinking hard every moment of the class, not only about the content but about themselves as people and as learners. Those are the bigger things I want to try to address this year -- hopefully by implementing "small" changes with big impacts.
So, I have in mind some things I want to do (they're not all such small changes, but I think they're manageable!):
* I am going to ask my new math colleagues to observe my teaching, and I am going to ask them right at the beginning of the year, before I have an opportunity to chicken out. I am going to schedule a teacher once every week in the beginning, and to ask them to observe me on a specific classroom goal I am trying to work on. For example, one of my classroom goals this year is to increase wait time and to facilitate effective whole-class discussions. I am going to ask my colleague to give me feedback specific to that, and also general feedback on the class and the lesson. Then, a couple of weeks later, I will ask a different colleague to come in, observe me on my wait time, and also to observe me on whether I am asking open-ended, exploratory questions and letting kids come to their own conclusions without me being The Authority. Then, a few weeks later, I'll ask a third colleague to come in and observe me on open-ended questioning and also how my kids are doing with meta-cognition. Eventually (ie. Semester 2??), I'll work my way to the bigger evaluation criteria, like the ones outlined in our rubric for mathematical practices.
Why am I doing this? It's two folds: 1. Obviously, as I have said, I want to get better at my classroom craft, and I know that having someone else in the room will help remind me that I'm supposed to be working on that actively. 2. I feel that it would be a great way to bond with my new colleagues and to show them by example that I value their input. Hopefully this will also open doors to talking about what we are doing in our classrooms, and hopefully if my colleagues see that I am comfortable asking for their direct feedback on my teaching, then they would feel comfortable down the road letting me observe their teaching as well.
* I am going to start a 4-people Critical Friends Group. At Klingenstein we rehearsed a protocol for reviewing lessons and/or a unit that you are struggling with. What I liked most about the protocol was that it removed subjectivity as much as possible and helped the person who is receiving feedback feel protected and not judged (well, if you stick faithfully to the protocol, that is). It also fosters cross-curricular feedback and collaboration, since these CFGs are typically made up of people from different departments (another way this protocol ensures you remain the "expert" of your domain and your colleagues are minimally judgmental and mostly supportive). I have already gotten an OK from one of the administrators to put out an announcement to all the staffers at the start of the year, to find 3 volunteers who are willing to be guinea pigs with me for a cycle of 4 rounds during Q1. Each of us would bring in something to share with the group -- something that we are genuinely struggling with and would like support/feedback on. If at the end of Q1 they all hate it, I'll ask for new volunteers and start a different group. If they like it, I'll break it into more groups and have them each facilitate a new group to help the idea grow at the school.
Why am I doing this? It's a way of taking PD into my own hands and to make sure (like this blog and general blog-reading does) that I am having quality reflections on teaching throughout the year.
* I am starting a new system for homework. It's a balance between letting kids have optional homework assignments but still using homework effectively as assessment tools. For each homework assignment, I am going to assign problems in all the following categories:
Why am I doing this? I agree with the SBG folks that kids should not be forced to do "busy" homework if they already get something, but I disagree that kids always know when they need that extra practice. I am going to make it explicit for them by providing homework solutions for all the problems (except the Extension and Teacher Assessment problems), and they can stop when they feel like they really get it with ease. The extension problems get kids to be used to working with/examining problems just beyond their reach. Teacher assessment is something I can have kids quickly write down numeric answers to on a sheet of paper (or hold up a whiteboard) at the start of class for me to assess where the class stands. This keeps homework meaningful for all of us.
* I am going to do weekly student feedback cards so that I can get ongoing, "formative" feedback as well.
* Allot time for meta-cognition. I want to do this early and frequently, so that it becomes part of the kids' routine during class. I wrote a separate blog post about some strategies for implementing this back in July, but obviously it could be less sexy methods, too, like building it into a worksheet.
* Once or twice each unit, I am going to build in "hinge points" into a lesson. We learned about this at PCMI this year, and it's something I am really missing in my classes. I am not going to go crazy with this, but a couple of times each unit I do want to create a lesson that can "hinge" one way or another depending on my on-the-spot assessment of where the kids stand. This way, lessons are not always so linear from A to Z, without taking into account kids' reactions in real time.
* I want to be more patient. One of the most powerful lessons I learned at KSI was that kids are learning from you every second in your presence. Am I being the adult that I want them to grow up to be, every minute of everyday? That's such a powerful question and one that I am afraid to answer, because the responsibility of it all seems daunting. I am going to try harder than ever to be that model adult every moment, every day.
Over the course of the summer, I've thought a lot about this list of changes and I believe it's a good, manageable one. It's ambitious, but most of it (except CFG) are small things that I can implement without changing EVERYTHING I am already doing, which is important to me. Wish me luck!
I think that as a slightly less newbie teacher now (I still feel very green, now going into my 6th year), I am at a different place in my career and my PD. I am fortunate to have had some great mentors along the way and some great resources for working on developing lessons that have worked out OK for me and the kids. Now I need to focus on my classroom craft, on how I ask questions, on building a better relationship with kids, on making sure that every kid is thinking hard every moment of the class, not only about the content but about themselves as people and as learners. Those are the bigger things I want to try to address this year -- hopefully by implementing "small" changes with big impacts.
So, I have in mind some things I want to do (they're not all such small changes, but I think they're manageable!):
* I am going to ask my new math colleagues to observe my teaching, and I am going to ask them right at the beginning of the year, before I have an opportunity to chicken out. I am going to schedule a teacher once every week in the beginning, and to ask them to observe me on a specific classroom goal I am trying to work on. For example, one of my classroom goals this year is to increase wait time and to facilitate effective whole-class discussions. I am going to ask my colleague to give me feedback specific to that, and also general feedback on the class and the lesson. Then, a couple of weeks later, I will ask a different colleague to come in, observe me on my wait time, and also to observe me on whether I am asking open-ended, exploratory questions and letting kids come to their own conclusions without me being The Authority. Then, a few weeks later, I'll ask a third colleague to come in and observe me on open-ended questioning and also how my kids are doing with meta-cognition. Eventually (ie. Semester 2??), I'll work my way to the bigger evaluation criteria, like the ones outlined in our rubric for mathematical practices.
Why am I doing this? It's two folds: 1. Obviously, as I have said, I want to get better at my classroom craft, and I know that having someone else in the room will help remind me that I'm supposed to be working on that actively. 2. I feel that it would be a great way to bond with my new colleagues and to show them by example that I value their input. Hopefully this will also open doors to talking about what we are doing in our classrooms, and hopefully if my colleagues see that I am comfortable asking for their direct feedback on my teaching, then they would feel comfortable down the road letting me observe their teaching as well.
* I am going to start a 4-people Critical Friends Group. At Klingenstein we rehearsed a protocol for reviewing lessons and/or a unit that you are struggling with. What I liked most about the protocol was that it removed subjectivity as much as possible and helped the person who is receiving feedback feel protected and not judged (well, if you stick faithfully to the protocol, that is). It also fosters cross-curricular feedback and collaboration, since these CFGs are typically made up of people from different departments (another way this protocol ensures you remain the "expert" of your domain and your colleagues are minimally judgmental and mostly supportive). I have already gotten an OK from one of the administrators to put out an announcement to all the staffers at the start of the year, to find 3 volunteers who are willing to be guinea pigs with me for a cycle of 4 rounds during Q1. Each of us would bring in something to share with the group -- something that we are genuinely struggling with and would like support/feedback on. If at the end of Q1 they all hate it, I'll ask for new volunteers and start a different group. If they like it, I'll break it into more groups and have them each facilitate a new group to help the idea grow at the school.
Why am I doing this? It's a way of taking PD into my own hands and to make sure (like this blog and general blog-reading does) that I am having quality reflections on teaching throughout the year.
* I am starting a new system for homework. It's a balance between letting kids have optional homework assignments but still using homework effectively as assessment tools. For each homework assignment, I am going to assign problems in all the following categories:
A: Self-assessment (You are expected to do this and make sure you can get the correct answer as provided. Show all work!)
B: Optional practice (If A was not completely straight forward, you should do these and check answers against those provided.)
C: Extension (Here's what's coming soon... TRY IT and let me see how far you get. Show all work!)
D: Teacher assessment (I want to see how many of you can get this correct. We're shooting for 100% on this! We'll review answers tomorrow in class.)
Why am I doing this? I agree with the SBG folks that kids should not be forced to do "busy" homework if they already get something, but I disagree that kids always know when they need that extra practice. I am going to make it explicit for them by providing homework solutions for all the problems (except the Extension and Teacher Assessment problems), and they can stop when they feel like they really get it with ease. The extension problems get kids to be used to working with/examining problems just beyond their reach. Teacher assessment is something I can have kids quickly write down numeric answers to on a sheet of paper (or hold up a whiteboard) at the start of class for me to assess where the class stands. This keeps homework meaningful for all of us.
* I am going to do weekly student feedback cards so that I can get ongoing, "formative" feedback as well.
* Allot time for meta-cognition. I want to do this early and frequently, so that it becomes part of the kids' routine during class. I wrote a separate blog post about some strategies for implementing this back in July, but obviously it could be less sexy methods, too, like building it into a worksheet.
* Once or twice each unit, I am going to build in "hinge points" into a lesson. We learned about this at PCMI this year, and it's something I am really missing in my classes. I am not going to go crazy with this, but a couple of times each unit I do want to create a lesson that can "hinge" one way or another depending on my on-the-spot assessment of where the kids stand. This way, lessons are not always so linear from A to Z, without taking into account kids' reactions in real time.
* I want to be more patient. One of the most powerful lessons I learned at KSI was that kids are learning from you every second in your presence. Am I being the adult that I want them to grow up to be, every minute of everyday? That's such a powerful question and one that I am afraid to answer, because the responsibility of it all seems daunting. I am going to try harder than ever to be that model adult every moment, every day.
Over the course of the summer, I've thought a lot about this list of changes and I believe it's a good, manageable one. It's ambitious, but most of it (except CFG) are small things that I can implement without changing EVERYTHING I am already doing, which is important to me. Wish me luck!
Monday, August 8, 2011
Engagement Thoughts
During the summer, when I was away from Geoff for 5 weeks, I thought about writing down some things that I loved about Geoff that even our friends may or may not know. Since we recently got engaged, it seems like an appropriate occasion for such a post! So, here we go. :)
I love Geoff because he is authentic. The first time I stayed over at his apartment, in the morning he put on a pair of circular, coke-can glasses. I politely pointed out that it's fairly unusual for someone to be so not self-conscious so early on in dating someone else. He shrugged and replied that people are either going to like you for who you are, or not. For that I liked him more.
I love Geoff because he has traits of a real gentleman. I know it's old-school, but he opens doors, carries my stuff, and plans a helluva good date. I also love that he is romantic and that we still hold hands everywhere we go. :)
I love Geoff because he is fiercely loyal. I see it in the way he treats his family and his friends. Even if things happen that show him that other people aren't as good to him as they maybe ought to be, he continues to give them 120% of his loyalty and goes out of his way to take care of them. I know that he does the same with me, and that sometimes I'm not as considerate as I ought to be. Geoff forgives because he is generous.
I love Geoff because he's hilarious. When you talk to Geoff, you never know when something phallic will seep into the conversation. (Usually within the first 30 minutes, if he really hits it off with a dude.) When we met my cousins for the first time (who are older than me and whom I had always looked up to as a kid), he was rubbing his nipples and sticking his tongue out at the lunch table. When he came back from Israel for the birthright trip, he told me that he had right away figured out the circumcision status of everybody in his birthright group. It's just the kind of thing he shares, and then people reciprocate; he's very disarming in a strange sort of way.
I love Geoff because when you talk to him, you feel like his attention zooms in on you and nothing else in the world matters for the moment. He's genuinely interested in what you have to say, and it's evident that people love talking to him.
I love Geoff because he's the only person I know who tries to make people underestimate him. Everyone else I know is out to prove themselves to the world -- how smart they are, how much money they make, how talented they are at XYZ. Geoff? You'd never hear him talk himself up at anything, even if he might be better than you at XYZ.
I love Geoff because he's the most methodical and disciplined person I know. He has so many checklists, that he has built entire software systems to keep track of the things he needs to do and his systems yell at him when things fall through the cracks or run behind schedule. Before he buys anything, he looks at hundreds of options, reads books, and creates entire spreadsheets and software systems to track things. Because of it, he makes superb life decisions and achieves big goals efficiently (even though only a few people know about these things).
I love Geoff because he has a creative soul. He's not the best guitar player, but every time he plays, he's writing and discarding new tunes. He thinks of our experiences in metaphors and sings about simple stories that have beautiful messages that are opaque unless you talk to him about them. I love that when Geoff sings, he sweats up a storm and you can picture a little Geoff singing out of a garage rock band.
I love Geoff because he is fearless. I've jumped off a cliff with him. I've slid down a steep volcano with him. I've climbed 7 floors of ladder-stairs with him. I've seen him stick his hand into a pot of hissing roaches. I've eaten live crickets with him. I don't think I would have done those things myself. He pushes me to always go a little bit beyond my comfort zone.
I love Geoff because he balances his wander-lust with his career ambitions. We've had numerous conversations about this, where we think it's quite amazing that neither of our careers suffers from our lifestyle, and that we have each other to share it with.
I love Geoff because he is a true optimist. He's so damned positive that I call him Positive Pedro (or just Pedro) most of the time, and he calls me (Negative) Nancy. He thinks everything is do-able, and doesn't stress out about anything. When Geoff's around, he sucks out all of the negative energy in the room and replaces it with the human equivalence of sunshine. :)
I love Geoff because he believes that what I do makes a difference in the world. At the end of a hard day, it's so good to come home to someone who believes you to be better than you are.
I love Geoff because even if I travel all the world, I may not find another person like him. We could never predict what things may come, but I am happy that we have decided that we will be in it together for the long haul.
I love Geoff because he is authentic. The first time I stayed over at his apartment, in the morning he put on a pair of circular, coke-can glasses. I politely pointed out that it's fairly unusual for someone to be so not self-conscious so early on in dating someone else. He shrugged and replied that people are either going to like you for who you are, or not. For that I liked him more.
I love Geoff because he has traits of a real gentleman. I know it's old-school, but he opens doors, carries my stuff, and plans a helluva good date. I also love that he is romantic and that we still hold hands everywhere we go. :)
I love Geoff because he is fiercely loyal. I see it in the way he treats his family and his friends. Even if things happen that show him that other people aren't as good to him as they maybe ought to be, he continues to give them 120% of his loyalty and goes out of his way to take care of them. I know that he does the same with me, and that sometimes I'm not as considerate as I ought to be. Geoff forgives because he is generous.
I love Geoff because he's hilarious. When you talk to Geoff, you never know when something phallic will seep into the conversation. (Usually within the first 30 minutes, if he really hits it off with a dude.) When we met my cousins for the first time (who are older than me and whom I had always looked up to as a kid), he was rubbing his nipples and sticking his tongue out at the lunch table. When he came back from Israel for the birthright trip, he told me that he had right away figured out the circumcision status of everybody in his birthright group. It's just the kind of thing he shares, and then people reciprocate; he's very disarming in a strange sort of way.
I love Geoff because when you talk to him, you feel like his attention zooms in on you and nothing else in the world matters for the moment. He's genuinely interested in what you have to say, and it's evident that people love talking to him.
I love Geoff because he's the only person I know who tries to make people underestimate him. Everyone else I know is out to prove themselves to the world -- how smart they are, how much money they make, how talented they are at XYZ. Geoff? You'd never hear him talk himself up at anything, even if he might be better than you at XYZ.
I love Geoff because he's the most methodical and disciplined person I know. He has so many checklists, that he has built entire software systems to keep track of the things he needs to do and his systems yell at him when things fall through the cracks or run behind schedule. Before he buys anything, he looks at hundreds of options, reads books, and creates entire spreadsheets and software systems to track things. Because of it, he makes superb life decisions and achieves big goals efficiently (even though only a few people know about these things).
I love Geoff because he has a creative soul. He's not the best guitar player, but every time he plays, he's writing and discarding new tunes. He thinks of our experiences in metaphors and sings about simple stories that have beautiful messages that are opaque unless you talk to him about them. I love that when Geoff sings, he sweats up a storm and you can picture a little Geoff singing out of a garage rock band.
I love Geoff because he is fearless. I've jumped off a cliff with him. I've slid down a steep volcano with him. I've climbed 7 floors of ladder-stairs with him. I've seen him stick his hand into a pot of hissing roaches. I've eaten live crickets with him. I don't think I would have done those things myself. He pushes me to always go a little bit beyond my comfort zone.
I love Geoff because he balances his wander-lust with his career ambitions. We've had numerous conversations about this, where we think it's quite amazing that neither of our careers suffers from our lifestyle, and that we have each other to share it with.
I love Geoff because he is a true optimist. He's so damned positive that I call him Positive Pedro (or just Pedro) most of the time, and he calls me (Negative) Nancy. He thinks everything is do-able, and doesn't stress out about anything. When Geoff's around, he sucks out all of the negative energy in the room and replaces it with the human equivalence of sunshine. :)
I love Geoff because he believes that what I do makes a difference in the world. At the end of a hard day, it's so good to come home to someone who believes you to be better than you are.
I love Geoff because even if I travel all the world, I may not find another person like him. We could never predict what things may come, but I am happy that we have decided that we will be in it together for the long haul.
Saturday, August 6, 2011
Germany: First Weeks
To put it mildly, Geoff and I have been very busy since our arrival in Germany 13 days ago. In those 13 days, I have: gone to the bank (twice) to start new bank accounts; gone to the school (twice) to do HR stuff and to meet my future administrators; registered with the city as a current resident and received a tax ID; seen a dentist/surgeon and made a follow-up appointment for wisdom teeth extraction for next week; gone to IKEA 3 times, in the rain, by subway and then a lot of walking each time (first time at IKEA, we were there for 8 straight hours, no joke); gone shopping at different stores nearly everyday for the apartment, since there is no equivalent of Walmart within subway reach of Berlin and our apartment needed fridge, washer/dryer, shower curtains, mirror in the bathroom, and everything else in between; run around to get our prepaid internet 3G stick/phones working; started to look for yoga studios and to explore our beautiful neighborhood; read two books on my new Kindle, and bought two more; confirmed that our permanent internet will be hooked up by early next week.
I know, that doesn't sound like a lot. It is. And that doesn't include building furniture, which Geoff pretty much did single-handedly (both because he's awesome and because he doesn't trust me to build our furniture).
First impressions of Berlin:
Anyway, that's it for now! I've got some big posts coming up. I'll get back to this Germany stuff later. Ciao!
I know, that doesn't sound like a lot. It is. And that doesn't include building furniture, which Geoff pretty much did single-handedly (both because he's awesome and because he doesn't trust me to build our furniture).
First impressions of Berlin:
* Beautiful bike lanes throughout the city
* German girls are oozing with style, even on rainy days -- this is the first place I've lived where girls look simply decadent and fabulous in their black stockings with big holes (not by design).
* Everything is so do-it-yourself. I ordered an ice cream softie and they gave me a token. I mistook it for a Euro dollar, and put it away. When I got to the machine with my cone, I realized while examining the machine that it requires a token to get started. You put your cone inside the holder, insert the token, and press a button to start the automagic making of a perfect swirl. That's one of many examples of how Germany is awesomely efficient.
* I cannot say that Berliners are very nice to foreigners who don't speak German. I really don't intend on being one of those assholes who speak English everywhere, but when I say, "Haben sie wein fur cooking?" I expect them to not yell at me for sucking at life. I cannot wait to have time to study German.
* My new coworkers, the ones I've met anyway, are very worldly and interesting. I am hopeful!
* The toilets are shaped funny. Really. Check out this article.
* There are outdoor markets and farmer's markets EVERYWHERE! yay!!
* Berlin has a lot of ethnic food. So far, I've had decent Vietnamese, Chinese, Thai, French cuisines, and some mediocre Indian, Tibetan, and Italian meals. There's a good falafel place just down the street from our apartment. And the cheese breads here are to die for! Brotchen mit kase!!
* As you would expect, the subway system is superb and runs on an honor system a lot like the lightrail system in Newark, NJ, where you get your ticket validated and the police only does pop checks for tickets, no turnstiles or anything. It makes me wonder what the overall loss/gain of profit is when you take away all those people who have to work full time at the NYC stations to monitor that no one is jumping the turnstiles, and you replace it with an honor system.
* One time fairly late at night, we had trouble getting home because all the trains were running on opposite tracks and only going for one stop because of construction. It was weird. Not something I would expect in Berlin. Even the locals were confused!
* On Sundays, everything closes. That's nice for two reasons: Everyone stays out until sunrise on Saturdays. You sleep in on Sundays until the afternoon, and then have a super lazy day afterwards.
* Here you can choose your electricity company from a list of various options (some are more eco-friendly than others but also cost more). And our "condense" dryer operates on humidity-sensor. In Germany, people really like to go for the natural stuff, so you can find Mango lassis on the street and people don't get general anesthesia for oral surgeries. I am discovering new things daily that remind me that I live in a first world country!
* Last but not least, I've been giving some thought to how we are all defined by our past, our present, and our future. My question (which will take me a while to answer) is how the current Germany is affected by its Nazi Germany past? Geoff asked someone about how many Jewish people live in Berlin. That person (a Berlin local) said that there are always German policemen stationed next to the Jewish schools for security reasons. Sadly, Neo-Nazis are still very much a real thing in parts of Europe, Germany included.
Anyway, that's it for now! I've got some big posts coming up. I'll get back to this Germany stuff later. Ciao!
Subscribe to:
Posts (Atom)