I recently got interested in the idea of exponential growth in the "real world," and a little bit of research got me thinking about the possibility of framing a math project surrounding the idea of exponential growth and (environmental or social) sustainability implications.
For example, one of the things that I spoke to my Algebra 2 students about is the idea that as our world population grows exponentially, so does our utilization of non-renewable resources, our CO2 emission rates, and our general waste emission. With technology also exploding exponentially (Moore's Law), our world economic output also increases exponentially. I dug up some statistics that the world economy grows, on average, 4% a year, which means that in one person's lifetime (less than 60 years), it'll multiple 10 folds. In a century, it'll multiply 50 folds. That's insane. Even if a part of this "growth" is due to inflation, the increase in our economic output is still growing substantially over time. The earth's finite resources cannot support even a steady linear growth, let alone a sustained exponential growth. The exponential pattern we experience now is simply not environmentally sustainable, and it points to the hypocrisy of our governments who simultaneously support environmental concerns and continued economic expansion.
Similarly, I did some digging on inflation rates, causes of inflation, and rises in public four-year university tuition as an example of inflation. The trend is exponentially increasing at a staggering rate, which comes back to a social justice issue, on the front of social sustainability. I told the students that the in-state tuition of UW is already twice as expensive now as when I attended university in California 10 years ago, and I was an example of a "regular" person who barely made it through college at those former tuition rates, working part-time and on financial aid. The more I think about it, the more I think that there is a prime opportunity here for an end-of-year project linking math and either social or environmental implications. Students can research data sets of their interest, create mathematical models, and then create a PSA to educate the school community about the social and environmental implications of such trends.
Thoughts? Have you done such a project and have resources that I can look at? I want to find a balance of leaving it completely open for them to choose something they care about, and providing some general framework to ensure it's going to be productive and meaningful. But, I've been thinking a lot about this! Brainstorming slowly for the end of the year...
Thursday, March 20, 2014
Saturday, March 15, 2014
Parametric Playground
I'm playing around with the idea of letting kids design and create an animation via parametric equations in GeoGebra. To play around with the idea myself, I tried to come up with some possible motions. Basically, I think that any motion that the kids can dream up, as long as it's a physically sensible pattern, we can create an animation via parametric equation.
Check these examples out: http://www.geogebratube.org/student/mnl0rUuxl . In this, I played around with a bouncing ball, a rotating circle, a rolling wheel, a dampened bouncing ball, and a ball that flies through air with downwards acceleration. In each case, there is an additional rotating point that stays with the circle as it moves around.
If they can dream it, they can create it! My thought is that they would design something, create it in GeoGebra via parametric equations, explain every part of their parametric equation, and plot x(t) and y(t) functions in terms of t (not by hand by via technology), and analyze some critical points along the graph.
Exciiiting!! I love projects like this, because as a baseline, it's reinforcing everyone's understanding of parametric equations, but the upper end is limitless to allow the creative and mathematically confident students to challenge the limits of their knowledge. For example, in order to create the dampened bouncing ball, I had to use the form y1(t) = a/(t + 1)*|sin(bt)| + c just to get the center of the ball to move/bounce in a dampened way, which made the height of the rotating point around the circle more complex:
y2(t) = csin(dt) + a/(t + 1)*|sin(bt)| + c .... In creating even something that looks simple, I incorporated rational, absolute-value, and sine functions. I would be very happy if some of my kids approached this level of complexity in their own projects.
Check these examples out: http://www.geogebratube.org/student/mnl0rUuxl . In this, I played around with a bouncing ball, a rotating circle, a rolling wheel, a dampened bouncing ball, and a ball that flies through air with downwards acceleration. In each case, there is an additional rotating point that stays with the circle as it moves around.
If they can dream it, they can create it! My thought is that they would design something, create it in GeoGebra via parametric equations, explain every part of their parametric equation, and plot x(t) and y(t) functions in terms of t (not by hand by via technology), and analyze some critical points along the graph.
Exciiiting!! I love projects like this, because as a baseline, it's reinforcing everyone's understanding of parametric equations, but the upper end is limitless to allow the creative and mathematically confident students to challenge the limits of their knowledge. For example, in order to create the dampened bouncing ball, I had to use the form y1(t) = a/(t + 1)*|sin(bt)| + c just to get the center of the ball to move/bounce in a dampened way, which made the height of the rotating point around the circle more complex:
y2(t) = csin(dt) + a/(t + 1)*|sin(bt)| + c .... In creating even something that looks simple, I incorporated rational, absolute-value, and sine functions. I would be very happy if some of my kids approached this level of complexity in their own projects.
Thursday, March 13, 2014
Creative Problem-Solving on the Rollercoaster Project
This is going to be a fuzzy-wuzzy post maybe. But, I wanted to write down how much I loved reading through the math work of my Calculus students, who completed those wonderful rollercoasters!
In the end, they took a variety of approaches:
* Some first chose the boundaries x = k, and then wrote down the boundary conditions f'(k) and f(k). They then took a generic form of the next adjacent function g, shifted it over to make g(x-k), and then differentiated g(x-k) and set g'(k - k) = f'(k), and g(k - k) = f(k) to solve for constraints on the remaining parameters in the g equation. In other words, they first chose boundaries, then did transformations, then got the derivatives to match via a standard algebraic approach (which we eventually, at the end of the project, went through as a class in preparation for their quiz).
* Some other students were clever. They first played with functions centered around x = 0, for example f(x) = ax^3, or f(x) = ae^x. They did this because it was easy to manipulate just "a" and the x value to get a numerical derivative and general shape that they wanted. For example, if they wanted a downwards parabola that connects with a derivative of 3, they might first get y = -x^2, and then figure that at x = -1, y' = -2(-1), so y' = 2. So, they figured that if they change "a" to be -1.5, then y' = 3. Bam, they got a general shape and a derivative value to match what they wanted at the boundary. And then all they had to do was to transform
y = -1.5x^2 over and up to the boundary, which is an easy task.
* Some other students chose their boundaries LAST. They first placed the pieces of functions down loosely, then took derivatives of connected equations and set the derivative equations equal f'(x) = g'(x). In their graphing calcs they solved for the x value where this occurs, and used that as the boundary x value. After that, they just shifted the g function up or down to meet the other function in height as well.
* Yet some other students used the principles of turning points to help them connect pieces. They also used horizontal symmetry around a vertex to predict steepness at a future part of a curve, etc.
* Many groups had trouble with ending their rollercoasters with the same height AND derivative value as in the very beginning. To help them make their lives easier, I recommended that they use the vertex form y = a(x - h)^2 + k on both ends, setting k to be the eventual height they wish to reach. They then had to put in an (x, y) value from the other boundary, and solve for a and h as a system. Even in doing this, there were some clever kids who did some clever substitution in order to make it easier to solve a rational system, while other kids turned it into a quadratic-linear system and solved graphically. Loved - it!
I felt really inspired by all of their individuality on this project. Even though it took a few more classes than I would have liked, I felt that the learning -- and moreover, the OWNERSHIP -- made it totally worth it in the end. Yeah!!!
In the end, they took a variety of approaches:
* Some first chose the boundaries x = k, and then wrote down the boundary conditions f'(k) and f(k). They then took a generic form of the next adjacent function g, shifted it over to make g(x-k), and then differentiated g(x-k) and set g'(k - k) = f'(k), and g(k - k) = f(k) to solve for constraints on the remaining parameters in the g equation. In other words, they first chose boundaries, then did transformations, then got the derivatives to match via a standard algebraic approach (which we eventually, at the end of the project, went through as a class in preparation for their quiz).
* Some other students were clever. They first played with functions centered around x = 0, for example f(x) = ax^3, or f(x) = ae^x. They did this because it was easy to manipulate just "a" and the x value to get a numerical derivative and general shape that they wanted. For example, if they wanted a downwards parabola that connects with a derivative of 3, they might first get y = -x^2, and then figure that at x = -1, y' = -2(-1), so y' = 2. So, they figured that if they change "a" to be -1.5, then y' = 3. Bam, they got a general shape and a derivative value to match what they wanted at the boundary. And then all they had to do was to transform
y = -1.5x^2 over and up to the boundary, which is an easy task.
* Some other students chose their boundaries LAST. They first placed the pieces of functions down loosely, then took derivatives of connected equations and set the derivative equations equal f'(x) = g'(x). In their graphing calcs they solved for the x value where this occurs, and used that as the boundary x value. After that, they just shifted the g function up or down to meet the other function in height as well.
* Yet some other students used the principles of turning points to help them connect pieces. They also used horizontal symmetry around a vertex to predict steepness at a future part of a curve, etc.
* Many groups had trouble with ending their rollercoasters with the same height AND derivative value as in the very beginning. To help them make their lives easier, I recommended that they use the vertex form y = a(x - h)^2 + k on both ends, setting k to be the eventual height they wish to reach. They then had to put in an (x, y) value from the other boundary, and solve for a and h as a system. Even in doing this, there were some clever kids who did some clever substitution in order to make it easier to solve a rational system, while other kids turned it into a quadratic-linear system and solved graphically. Loved - it!
I felt really inspired by all of their individuality on this project. Even though it took a few more classes than I would have liked, I felt that the learning -- and moreover, the OWNERSHIP -- made it totally worth it in the end. Yeah!!!
Friday, March 7, 2014
Rollercoaster project SUCCESS!
And (drum rolls), here are all the other rollercoaster projects! They are wonderful!
The basic requirements are that they must have 5 segments, and it must be smooth and continuous at all points. The leftmost and rightmost x values must match in their function and derivative values, in order to form a loop!
The basic requirements are that they must have 5 segments, and it must be smooth and continuous at all points. The leftmost and rightmost x values must match in their function and derivative values, in order to form a loop!
Thursday, March 6, 2014
Rollercoaster Sweetness
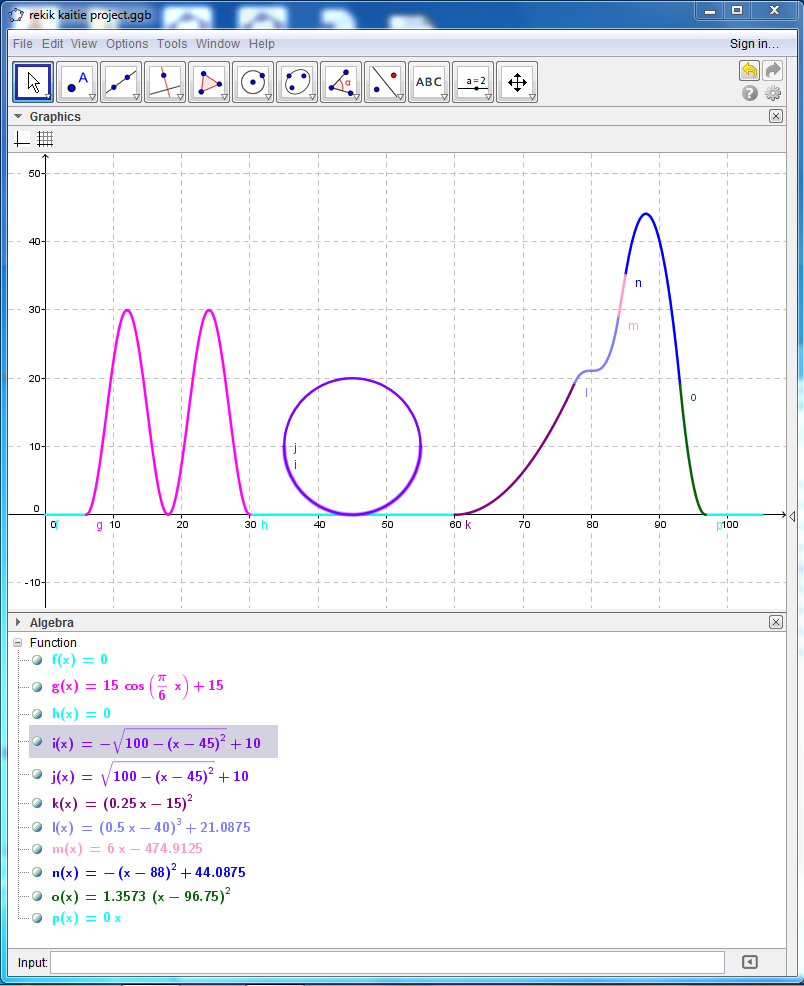
The first Calculus rollercoaster project file has come in! It looks like this:
Not bad! Let's hope all the other ones will look like this tomorrow. I'll be verrrrry happy. They're also supposed to turn in a 3-D form of this, whereby they draw their curve on poster board, cut it out, and glue the two ends (leftmost x and rightmost x) together to form a sort of loop. That's why their leftmost and rightmost function and derivative values also need to match up. And they need to turn in either calculation work leading up to the equations, or an explanation of how they did it.
Hurray to the end of an era. Next week, we will start another project!
Not bad! Let's hope all the other ones will look like this tomorrow. I'll be verrrrry happy. They're also supposed to turn in a 3-D form of this, whereby they draw their curve on poster board, cut it out, and glue the two ends (leftmost x and rightmost x) together to form a sort of loop. That's why their leftmost and rightmost function and derivative values also need to match up. And they need to turn in either calculation work leading up to the equations, or an explanation of how they did it.
Hurray to the end of an era. Next week, we will start another project!
Subscribe to:
Posts (Atom)