Some Juicy Problems from Exeter Math 3

When I was at Klingenstein Summer Institute, I met a rock star math teacher who showed us a video of her kids working on Exeter problem sets. She just lets them work at their own paces, and when they're done, they decide who's going to go up to the board to put up their solutions, and then they discuss the differences and decide together what the correct answer is. The entire time during the class discussion, she says close to nothing! It was amazing. The level of engagement and self-start from her kids was mesmerizing and very inspirational.

In the real world, we all have our own state-mandated or school-mandated curricula to cover, but I've heard so many good things about this Exeter thing that I decided to try to work through one of the books to see for myself what this Exeter fuss is all about. Then, life got crazy and I didn't have time to do this. So far, I've only done a little over 70 pages of Math 3, even though my original intention was to do all of Math 3 before school starts. And thus far, my impression of the Exeter problem sets is that they feel a lot like the PCMI problem sets. The problems escalate in complexity and connections between skills from the beginning of the book to its end. Within each page, the problems are not all related to the same topic, thereby forcing kids to really think about which older concepts connect to this one. It moves nicely along the spectrum from the concrete to the abstract; it is evident by the sequence of problems that certain concepts the students are expected to develop independently of the teacher's instruction. Other concepts (such as 3-D vector math and relationships between points, lines, planes in 3-D space, or parametrized equations) I feel that the teacher would need to intervene more heavily to bridge the gaps between the pages. Regardless, the problem sets constantly push students to be independent problem-solvers, and each algebra skill is introduced while embedded in deeper connections. Some of the probability problems can also be readily changed to into experiments, which is delightful to me. :)

I also noticed, at least for me, that the problem sets were tediously slow in the beginning, as I tried to rack my brain to figure out which math concepts in my past applied to these situations I had never seen before. 70 pages later, I can skim a page and only stop to do one problem to make sure that I can do it. I am sure your kids would speed up as well, as they move through the pages and begin to connect concepts more effortlessly.

I found it useful along the way to keep track of the juiciest problems, because then regardless of what curricula I teach, I can pull out and adapt those juiciest problems to my own classes. I am not sure how much time I will have in the upcoming weeks to finish up the task I had started, so I'll share what I have right now, hopefully just in time for some of your upcoming math units. If you're Facebook friends with me, the first few problems should look familiar... Exeter owns all the credit for this material, obviously, but they are very generous in sharing their problem sets publicly, so I don't feel so bad about re-posting them here.

Here we go, some of my favorite problems thus far:

There are two circles that go through (9, 2). Each one is tangent to both coordinate axes. Find the center and the radius for each circle. Start by drawing a clear diagram.

----

Find the total grazing area of the goat G represented in the figure (a top view) shown at right. The animal is tied to a corner of a 40' × 40' barn, by an 80' rope. One of the sides of the barn is extended by a fence. Assume that there
is grass everywhere except inside the barn.

----

Point by point, a dilation transforms the circle x² − 6x + y² − 8y = −24 onto the circle x² − 14x + y² − 4y = −44. Find the center and the magnification factor of this transformation.

(Continuation) The circles have two common external tangent lines, which meet at the dilation center. Find the size of the angle formed by these lines, and write an equation for each line.

----

A coin of radius 1 cm is tossed onto a plane surface that has been tesselated by right triangles whose sides are 8 cm, 15 cm, and 17 cm long. What is the probability that the coin lands within one of the triangles?

----

To win the carnival game Ring Ding, you must toss a wooden ring onto a grid of rectangles so that it lands without touching any of the grid lines. The ring has a 3-inch diameter, the rectangles are twice as long as they are wide, and the game has been designed so that you have a 28% chance of winning. What are the dimensions of each rectangle?

----

Let A = (0, 0, 0), B = (9, 8, 12), and C = (6, 2, 3). Find coordinates for the point on line AB that is closest to C.

----

The diagram below shows a rectangular solid, two of whose vertices are A = (0, 0, 0) and G = (4, 6, 3). Find the point on segment AC that is closest to the midpoint of segment GH.


----

Let A = (−7,−4) and B = (7, 4), and consider the fact that the dot product of vectors PA and PB is zero. Describe the configuration of all points P = (x, y) that fit this requirement.

----

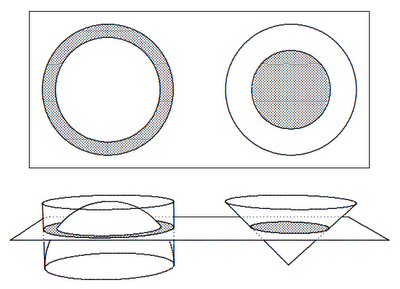A hemisphere of radius 8 is inscribed in a cylinder of radius 8 and height 8. The figure shows top and side views of the hemisphere, the cylinder, and a cone whose radius and height are both 8, and whose base and vertex are coplanar with the bases of the cylinder.

Consider that part of the cylinder that is outside (above) the hemisphere. Slice this region by a plane that is parallel to the cylinder base and 5 inches above the equator of the hemisphere. The intersection is a ring between two concentric circles. The same plane slices the cone, creating a disk. Show that the ring and the disk have the same area.

(Continuation) Suppose now that the three radii and two heights are all r. Show that the ring and the disk have the same area, no matter what the height of the slicing plane.

(Continuation) If the cone were filled with liquid, it could be poured into the cylinder, which still has the hemisphere stuck in the bottom. Will all the liquid fit? Expressed in terms of r, what is the volume of the cone? of the empty cylinder? of the hemisphere?

(Continuation) Show that a sphere of radius r encloses a volume of (4/3)πr³.

----

The rectangle shown has been formed by fitting together four right triangles. As marked, the sizes of two of the angles are α and β (Greek “alpha” and “beta”), and the length of one segment is 1. Find the two unmarked angles whose sizes are α and α + β. By labeling all the segments of the diagram, discover formulas for sin(α+β) and cos(α + β), written in terms of sin α, cosα, sinβ, and cosβ.

----

Imagine covering an unlimited plane surface with a single layer of pennies, arranged so that each penny touches six others tangentially. What percentage of the plane is covered?

----

The table shows the results of a probability experiment. Forty-eight dice were rolled, and each die that showed "2" on top (a deuce) was removed. The remaining dice were rolled again, and deuces were removed. This procedure was repeated until all the dice were gone.

Each entry in the left column is a roll number. The corresponding entry in the right column is the number of dice that had not yet turned up deuces after this roll.

These variables are not linearly related. What happens if you try to apply logarithms to straighten this data?

(Continuation) If forty-eight dice are rolled once, how many do you expect to remain after removing the deuces? How many dice do you expect to remain after two applications of the above procedure? After ten applications?

(Continuation) If a prize were offered for predicting how many rolls will be needed to remove all 48 dice, what would your guess be? Explain.

----

The figure at right shows an outermost 1 × 1 square, within which appears an inscribed circle, within which appears an inscribed square, within which appears another inscribed circle, within which appears another inscribed square. Although the figure does not show it, this process can be continued indefinitely. Let L₁ = 1 be the length of a side of the first (largest) square, L₂ be the length of a side of the second square, L₃ be the length of a side of the third square, and so on. Show that the numbers L₁, L₂, L₃, ... form a geometric sequence, and calculate L₂₀.

(Continuation) Let A_n be the area of the nth square. Is the sequence A₁, A₂, A₃, ... geometric? Explain.

----

When the note middle C is struck on a piano, it makes a string vibrate at 262 cycles per second. When the corresponding note one octave higher (denoted C') is struck, it makes a string vibrate at 524 cycles per second (twice as fast as the first string). These two numbers form part of a geometric sequence of frequencies
. . ., C, C#, D, D#, E, F, F#, G, G#, A, A#, B, C', . . .

known as equal-tempered tuning. Given C = 262 and C'= 524, find the frequency of G, and the frequency of the note that is n steps above middle C. (For example, F is 5 steps above C.)

(Continuation) Without calculating any of the indicated frequencies, explain why the ratio G:C is the same as the ratio A:D, which is the same as the ratio B:E. Now calculate the ratio G:C and show that it is approximately equal to 3:2, the musical interval known as a fifth. The disagreement between the two ratios is why some violinists do not like to make music with pianists.

----

On the same system of coordinate axes, graph the circle x² + y² = 25 and the ellipse 9x² + 25y² = 225. Draw the vertical line x = 2, which intersects the circle at two points, called A and B, and which intersects the ellipse at two points, called C and D. Show that the ratio AB :CD of chord lengths is 5:3. Choose a different vertical line and repeat the calculation of the ratio of chord lengths. Finally, using the line x = k (with |k| < 5, of course), find expressions for the chord lengths and show that their ratio is 5:3. Where in the diagram does the ratio 5:3 appear most conspicuously? Because the area enclosed by the circle is known to be 25π, you can now deduce the area enclosed by the ellipse.

(Continuation) What is the area enclosed by the ellipse x²/a² + y²/b² = 1?

----

The Hoyts company has a fleet of 1000 cars for one-day local rentals, which must be leased from either the Exeter office or the Hampton office. The company expects that 70 percent of the cars rented in Exeter return to the Exeter office, 60 percent of the cars rented in Hampton return to the Hampton office, and all cars return to one office or the other. Assume that all 1000 cars are rented each day, and that 200 of the rental cars are in Exeter and 800 are in Hampton on Monday morning.
(a) What distribution of cars is expected on Tuesday morning?
(b) What distribution of cars is expected on Wednesday morning?

(Continuation) Verify that the equations

E₀ = 200
H₀ = 800
E_n = 0.70E_n-1 + 0.40H_n-1
H_n = 0.30E_n-1 + 0.60H_n-1

provide a recursive description of the rental-car distribution.

(a) What information do the last two lines convey when n = 1?
(b) The last two lines could be written in matrix form as
.
Verify this. Then find a 2×2 matrix M so that [E_n H_n ] = [E_n-1 H_n-1 ]M.

(Continuation)Let v = [200 800] be the initial distribution of cars. Thus vM is the distribution of cars on Tuesday morning.

(a) What does the matrix product (vM)M = vM² represent?
(b) What does the matrix product vM¹⁰ represent?
(c) Matrix M is an example of a transition matrix. After you label its rows and columns, interpret the entries of M as probabilities.
(d)The sum of the entries in each row of M is 1; how is this significant?

(Continuation) Solve the equation [x 1000−x]M = [x 1000−x]. Interpret.

----

The reflection property of parabolas. Let F be the focus of a parabola, and let P be an arbitrary point on the parabola. Let μ be the line through P that is parallel to the axis of symmetry of the parabola; this means that μ intersects the directrix perpendicularly at a point N. Let λ be the perpendicular bisector of FN.

(a) Explain why P is on λ.
(b) Explain why λ is tangent to the parabola.
(c) Explain why λ bisects angle FPN.
(d) Justify the title of this problem.

---

A typical long-playing phonograph record (once known as an LP) plays for about 24 minutes at 33 1/3 revolutions per minute while a needle traces the long groove that spirals slowly in towards the center. The needle starts 5.7 inches from the center and finishes 2.5 inches from the center. Estimate the length of the groove.

----

On 1 July 2011, you deposit 1000 dollars into an account that pays 6 percent interest annually. How much is this investment worth on 1 July 2031? Before you turn your calculator on, write a calculator-ready expression for the answer.

(Continuation) On 1 July 2012, you deposit 1000 dollars into an account that pays 6 percent interest annually. How much is this investment worth on 1 July 2031? Answer the same question for deposits made on 1 July 2012, 1 July 2014, and so forth, until you see a pattern developing in your calculator-ready expressions.

(Continuation) Suppose that you deposit 1000 dollars into the same account on 1 July every year. The problem is now to calculate the combined value of all these deposits on 1 July 2031, including the deposit made on that final day. Rather than getting the answer by tediously adding the results of twenty-one separate (but similar) calculations, we can find a shorter way. Let V stand for the number we seek, and observe that

V = 1000(1.06)⁰ + 1000(1.06)¹ + · · · + 1000(1.06)¹⁹ + 1000(1.06)²⁰

is the very calculation that we wish to avoid. Obtain a second equation by multiplying both sides of this equation by 1.06, then find a way of combining the two equations to obtain a compact, easy-to-calculate formula for V .

(Continuation) Any list first, first·multiplier, first·multiplier², . . . , in which each term is obtained by multiplying its predecessor by a fixed number, is called a geometric sequence. A geometric series, on the other hand, is an addition problem formed by taking consecutive terms from some geometric sequence. Two examples: 16 + 24 + 36 + 54 is a four-term geometric series whose sum is 130, and 32−16+8−4+· · ·+0.125 is a nine-term geometric series whose sum is 21.375. Consider now the typical geometric series, which looks like first + first·multiplier + first·multiplier² + · · · + last. Find a compact, easy-to-calculate formula for the sum of all these terms.

PS. To save you some googling, you can access the entire Exeter Math 3 text here.