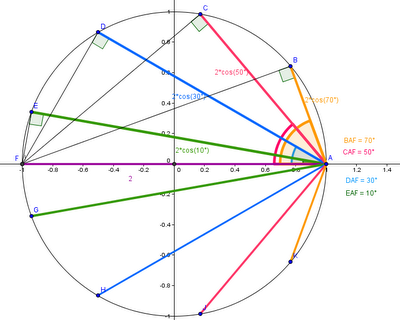

Of course, I leave it to you to find out what the products would be. (Not difficult, obviously, considering all the lengths are already labeled for you.) What's getting me stuck is how to simplify this process into one neat formula, given any n, in order to prove the conjecture. (If you click through Sam Shah's post, you'll see at the bottom that I tried to formulate it at least in words, but my calculus fails me and I'm not sure how to write down one elegant formula for the whole thing!)
Anyway. I thought I'd share it with you, especially because GeoGebra helped me make such nice unit-circle diagrams, complete with color-coding! :)
--------------------
Incidentally, I've been (true to my word) researching Geometry stuff for next year. In particular, Nancy Powell has some really lovely Geometry projects, that seem extremely rigorous and FUN! This was the first link that I came across when googling Geometry projects, so it's probably old news... but in case you haven't seen it, you MUST check it out!!
And, here is a cute SAT problem from David Marain -- this one is good for your middle-schoolers (and/or good for discussions about prime factorization)! :)

Hey there!
ReplyDeleteI just discovered your blog today (through one of your comments on an old Math Stories blog post) and I love it!
Do you twitter? I would like to follow you there also :)
Thanks!
@Mrs_Fuller
Hi there! Thanks! I'm new to this whole edu-blogging thing, but I'm trying to get some momentum going before school starts. :) I don't twitter (for now, anyway), but I plan on blogging regularly.
ReplyDeleteWhat levels of math do you teach? What did you find interesting here? I've taught Algebra 1 (middle-school), Geometry, and Algebra 2, and I'll be picking up a section of Precalc this year, so my interests are varied...
I was looking at your solution and thought it was ingenius, a good geometric approach! You maybe able to generalize it if you notice (using the fact that the central angle is equal to twice the inscribed angle.
ReplyDeleteoops. heh, if you notice that these angles evenly spaced. You would get:
ReplyDelete2^n (product from i=1 to n of abs[sin(360i/2n)])
Hi Bundy! Thanks for dropping by. I realized the connection between inscribed and central angles, and essentially my "solution" states that, although in a roundabout way. I'm hoping for a way of simplifying it further to show why 2^n times the product of all those sines always equals a beautifully simple n at the end. But, if you go back to the original thread, at least all the other mathies who used trig were stuck on the same step. Only one person was able to breakthrough the bottleneck, but not with trig. (He used the fact that x^n = 1 has n solutions equally placed along the unit circle, but it's unclear what he did after that).
ReplyDeleteAnyway, I'm glad you enjoyed this approach! I think parts of this problem is still adaptable to high school kids, although not all of it.