Teaching Number Definitions Meaningfully

As a kid, I was never good with mathematical terms. I was always doodling in math class and only picked up vocabulary words osmotically (which also meant not so effectively). As a teacher, I have tried to make vocab instruction more meaningful for kids.

Recently, in Grade 8, we started talking about inequalities for the first time. I started off the discussion by asking kids to give me some examples of equalities, and we wrote them on the board. After a few minutes, we started to list examples of inequalities and I went over why in math, saying -5 is less than -2 is a bit more precise/less confusing than saying -5 is smaller than -2.

Then, I asked the kids to come up with some example numbers that can satisfy the inequality
x + 2 < 15 . The kids started to list numbers, and after a few minutes I asked them for what they wrote down, and in the context of this we discussed number types. I explained to them that I think generally, in life, when you want to brainstorm options in your head, you don't want to keep listing the same types of objects over and over again, because in doing so you are limiting your vision of what is possible. The examples that the first kid gave me were {1, 2, 3, ..... , 12} and the examples that the second kid gave me were {-1, -2, -3, -100}

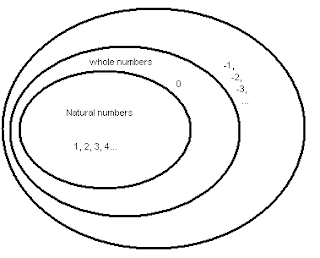
I drew on the board this diagram and said that "a long time ago, when cave people started counting sticks on the ground, they came up with numbers like 1, 2, 3, 4... These were called natural numbers.* Then eventually they came up with one more number to add to that set, and they called it whole numbers. Can you guess what that new number was?"

After kids enthusiastically guessed zero, they were starting to understand this diagram representation of a subset and were beginning to appreciate the historical development of numbers. Then, I added another layer of negative numbers and asked them what that is called when we started at some point to include/consider negative numbers as well.

They figured out that it was called integers. Great!

Then, I asked them what types of numbers they still know / have learned that we haven't named yet. They gave examples of decimals and fractions, and we added them to this picture.

In the end, we went back to the original topic at hand of finding example numbers that satisfy the inequality x + 2 < 15, and this time they were much better equipped to list a variety of examples and to discuss the full range of (non-discrete) solutions, which then led to the discussion of shading the solutions on the number line, and why we need the open circle rather than the closed circle sometimes.

I find this to be a more natural way to teach number types. Another time when I have done this was in teaching 9th-graders how to think of possible counterexamples that might disprove a math statement. If in their heads they are only considering a single type of example, then they're not being effective and thorough in their consideration of possibilities. As a kid, I would have appreciated this type of instruction of categorical types, followed immediately by application of its usefulness, and it would have probably helped me remember the names better. So, for me as a teacher, I always think it is important that I don't introduce the number definitions purely in isolation just because it's part of section 1.1 in the textbook. In the end, our teaching of these numerical categories should be explicitly supporting the kids' thinking, rather than just to add to the volume of disconnected rote knowledge in their heads...

*Note: By the way, I prefer this definition of natural numbers, even though I know that mathematicians don't all agree. Some refer to zero as part of the natural number set.