Grade 9 Videos Review Project

I am learning from a not-great experience with having kids create videos to recap the skills that we had learned during the first semester. I'm jotting it down here so that you can read about how it went and help me to make it better next time.

I still think the idea was good. We had done so much great multi-stepped, contextual algebra practice during the first semester (with my "low" Grade 9 class), that I didn't want them to just leave it all behind as we move on to new Geometry topics in the second semester. I didn't want to have to come back in June to re-teach them everything they knew, but I knew that retention would always be a problem for these kids.

So, I came up with the idea that we'd divvy up all the topics from the first semester, and each group would be responsible to make some explanatory videos on one topic. They'd upload the videos to the web, and I would provide links for all the kids to access these instructional videos. Then, during Spring Break, I'd assign as vacation homework for the kids to watch each other's videos and to do just two or so practice problems related to each video. This way, they're somewhat refreshed on the old concepts over time, and it also takes the pressure off of me as the "all-knowing info source" when it comes to review time.

Sounds good in theory, except I totally underestimated what a huuuuge task this would be for a group of kids who cannot really self-monitor their progress very effectively. They really did try; that I am impressed by. I had helped them prepare for the filming last week prior to leaving for the AGIS Conference, in hopes that they could just use my day of absence to film their videos on the iPads and to upload them. Little did I know that it was not going to be so easy. When I got back this week and looked at the videos, I was pretty disappointed. Most of their videos either had inaccurate mathematics, or the problems they picked were too easy (or, sometimes, too ambitious). I blame that on myself; if you want it to be done right, you simply have to closely supervise the kids in order to give them just-in-time feedback as they are filming and pulling those last pieces together. So, today in class I gave them another 80 minutes to re-do and re-do their mathematics and their videos. This time, I checked in with every group to make sure that their math was production-ready by the time they started filming. Even then, they still had to repeat the filming a bunch of times just to avoid all the careless mistakes. It was just so tough for them to master the simultaneous communication and solving of a multi-stepped problem. In the end, it was really good practice for them to zoom in on their own mistakes and to keep re-doing to correct them, even though the final video quality was not great. (On the iPads, the audio and the video are both of weak quality.) Fortunately, since the kids had mostly selected (with my help) the topics that they had individually struggled with on the semester test, this was a great remediation strategy for them to have to create these explanatory videos, regardless of video quality.

In the future, I really need to think carefully about what technology to use, how to set up the room so that different groups can be filming at the same time, how to help them rehearse prior to filming, etc. There is too big of a range between groups who put in a lot of effort into this project to make a good video, and those who just kind of slapped something together and called it a day. I also need to think about the timing, because unfortunately, this project takes too much time in class, as the kids need support all the way through (including the filming parts) and part of me just wants to move on to new topics already, knowing how much ground we still have to cover.

It's quite a shame that this project didn't work out to have superb products, because I think the process was definitely worthwhile and many of the kids learned a fair amount while doing this. It was definitely challenging for them, and I think some of their frustration came from how challenging this task was. I have hope though, that with some restructuring, I can find a way to make this work much better the next time. One of the restructuring ideas I had, for example, was that instead of everyone doing review videos all at once after a whole semester, after each unit I'd pick a small group of students (who had performed weakly on the exam) to do the videos for just that recent topic. This will ensure that timing is less of an issue, because they'd just work on it outside of class with my help, say at lunch time, and it'd also ensure more immediate remediation. I would also be able to ensure the videos are of better quality, since I am only focusing on managing one group at a time. Have you ever done something like this? Can you share any tips with me to make this a more successful experience in the future?

Addendum: Here are a few samples of produced videos. http://bit.ly/linesReview1, http://bit.ly/linesReview2, http://bit.ly/linesReview3, http://bit.ly/anglesReview1, http://bit.ly/anglesReview2. The kids in my "low" group had to create videos for lines, quadratics, midpoint/distance word problems, drawing geometric diagrams, and analysis of angles. Blip.tv only lets me upload 3 videos each day, so I'll post more links later!

Intensive Feedback for Every Kid

I have said this before and I will say it again: I find that mini whiteboards are wonderful in giving immediate feedback to students and receiving immediate feedback from them. This year, after I started using mini-whiteboards on a semi-regular basis in Grade 7, I have seen my students growing leaps and bounds in their accuracy. They absolutely love those lessons because they love to be recognized for being correct. (I usually say after a complicated problem, "Pat yourself on the back if you got that one completely correct." They love patting themselves on the back. heehee. And come on, who doesn't?) By now they're used to the idea that when I say something during the lesson, it is going to help them during the mini-whiteboard practice, so their ears actually perk up to listen. That is night-and-day compared to their attention span on other days.

In one 80-minute lesson last week, we reviewed: multiplying a 2-digit number by a 1-digit number in our heads; finding the common denominator of two fractions like (3x + 5)/24 = (6 - 2x)/7 as an application of this arithmetic skill; cross-multiplication and why it works (this was following DAYS of fractional equations practice, so I felt that at this point they were ready to bypass the denominator part and ready to see why the numerators would change as such); solving various proportional equations using cross-multiplication; solving percent word problems using proportions. In fact, they were so great with this exercise that they were able to figure out that something like (3x - 5)/6 = (2x + 7)/4 would have no solution, which is a topic from a while ago that I just threw in to the mix.

In one lesson, basically all the kids practiced and understood all of these skills. Of course we'll go back to individual/paired practice this week as we build up towards a formal assessment, but having their intensely focused attention for 80 consecutive minutes and receiving/giving constant individual feedback from/to every kid is simply priceless. It does wonders for their progress towards mastery.

In fact, the word has gotten out that I use these mini whiteboards regularly and that I love them... Other-subject teachers on my floor have started to borrow them from me to use in their classes. Great!

...Wow. We're so ready as a class to move on from basic algebra to explore basic geometry. I can actually feel the anticipation! :)

Gestures, Language, and Student Understanding

I went to a fabulous AGIS session this morning on sign language in the elementary classroom. It was led by Armin Martin and Johnnie Wilson from the Munich International School. They showed videos of kids who use their hands to touch different parts of their heads (front, back, left, right, top, bottom), in order to figure out how many "faces" a cube has. The kids are able to link the mathematical word "face" to layman's definition of "face", in order to bridge the gap between the concepts.

A very interesting point that was made during this presentation was that signs can be used as an intermediary between normal language and academic language, or between home language and school-instruction language. Intentional incorporation of appropriate signs can be a strategy that works not just with our ESL / EAL population but even with our normal kids, and it ties nicely into math because when you gesture in space, you are quickly illustrating and bringing in extra dimensions that are hard to do/experience on paper. The presenters presented research that said that even when you later take away the gestures, the kids still retain the primitive, physical understanding that they had achieved through gesturing. So fascinating, because this discussion/session got me thinking about a lot of different things that previously I had thought to be disconnected:

1. Recently my 7th-graders have been working on percent word problems such as "64 is 40% of what number?" Sure, some kids can easily navigate the proportional reasoning --> 10% of that number must be 16, so 100% of that number must be 160. But, for many kids they need a different strategy, and so we have been practicing setting this up as a proportion. Even then, for kids to read a problem like this and then to consistently set it up correctly, is not trivial. They need to be able to:

a.) Parse the verbal description.
b.) Correctly associate the value given (in this case, 64) with either the fractional percent (in this case, 40%) or the whole (100%).
c.) Set up proportion accordingly.
d.) Solve algebraically.

Of this, part B is the most difficult for 7th-graders. I found this year that when I went around to conference with kids about this process and to help them get started on the assignment, I can just point at the value within the problem (64), and then gesture to them using distance between my hands to ask, "Is this the part or the whole?" This has helped them tremendously, because they can associate the rather multi-stepped numerical operations to a simple visualization, and then they only need to focus on part A (re-reading the question to themselves) in order to make that determination and to carry out the rest of the steps by themselves. This simple gesturing was able to shrink my conference time with each kid to under 1 minute; they immediately would say, "Oh, I get it now," and then proceed with the other questions which were not always phrased in the same way or giving the same information. ("42 is what percent of 70?"  "What is 20% of 95?" etc.)

2. When I taught 8th-grade back in New York, I taught one particular 8th-grader who was very economical with his words. I would always put explanation questions on the test, and he was so concise with his explanations that he could always write down the correct answer in about half of the word that I would need to use. This is an incredible skill, because in order to do this, the kid needed to:

a.) Know/master the concept and relevant vocabulary.
b.) Prioritize information in his head.
c.) Formulate his understanding in as few words as possible using the prioritized list.

3. I have read somewhere that babies can already understand physical rules in the world. If you play an optical illusion on them that is against their normal experience, they will keep staring at the place where the ball disappeared after dropping. At this stage, their understanding is far beyond their ability to verbalize it. So, I think it is definitely true that we understand a lot more than our words are able to describe, especially at a young age or as a language-learner.


So, in short, I think gestures are a fabulous way to help kids understand concepts when their language is not yet developed enough to explain or describe a concept (old or new) fully. But, this intentional incorporation of gestures should lead in mathematics to a formalization of those concepts, and attachment of specific language. Because in doing so, we are teaching the value of specificity and prioritization, which are very important skills for the older students to have/develop in the long run.

Hope this little reflection was helpful to you in jogging your brain about how to bridge abstract concepts quickly to visual/kinesthetic understanding for kids. Please share with me if you have had similar success in other examples of utilizing intentional gestures to build intuitive understanding!

AGIS - Day 2; plus, my presentation!

Day 2 of the AGIS conference was great! In the morning, I went to a lovely elementary math presentation done by Beth Winkler from Bonn International School. She is the math subject leader at her school and they do some wonderful investigative things with their kids. She was able to show us various subtraction algorithms, for example, that the kids developed together with the teacher, and to talk about how they structure always two content strands (ie. Numbers and Data/Stats) to run in parallel during any given week. Numbers strand (ie. numeracy and numerical operations) is taught and practiced more or less in isolation (facts are reinforced with games), and the second math strand (such as Data/Statistics) is incorporated into their current PYP themed unit. For example, for the PYP unit "Body Systems," they had kids measure a bunch of their body parts and to do statistical analysis on the results. They also let kids' own curiosities direct them in the direction of mathematical inquiry. Recently, they realized through one such inquiry that the girls' shoes and boys' shoes in the class have the same mean size (length), but the girls' shoes have a smaller range in size than the boys. So, the boys' claim (which was the reason for this mathematical investigation) that "Girls in our class have smaller feet!" isn't really true! How terribly cute and engaging. They also have set periods of math, to ensure that the same amount of math is covered in every grade / class, which can sometimes be a challenge for PYP schools where everything is taught in themes.

Moreover, just the way this lady talked about math was wonderful. She really wanted to focus on helping kids not to be afraid of math, and she understands how to apply concrete-to-abstract continuum in math education, not just within each lesson, but over the years. She made me really wish that our school could have such a subject specialist at the elementary level. It's something I have asked for on behalf of our department, but I don't know if there is such room in our budget to hire such a specialist. Maybe. We will have to see as the 2013-2014 budget slowly takes its shape.

Then came my own presentation! I was very nervous, to be honest. But, the presentation was very well-received by my very small audience (only about 10 people, which is a shame because there were more math people who had wanted to be there, but the session was "maxed out" on paper and so they hadn't signed up...). Everyone came up to me afterwards and said that they thought it was very interesting, even the elementary teachers and one of my own departmental colleagues. They said that they thought there were definitely ideas that they took away that they think they can adapt for their classrooms, which was wonderful because it was my first out-of-school presentation!

Here is the presentation link: http://bit.ly/AGIS2013projs It's meant to be viewed in Slideshow mode, so that you can navigate all the embedded links to slides that make this a presentation that can adjust to audience's interests in real-time. But, in the notes section of the presentation I wrote more verbose descriptions about each slide. During the presentation, I opened one external document (the directions of the 3-D project), to discuss it in details in order to let the teachers see exactly how it would be structured in my class.

Then, after my own presentation I went to a fabulous one on elementary Fun and Games. The teacher is a New Zealander, and she demonstrated various games from New Zealand Math(s) that I thought were very simple in format and easy to adapt to younger or older age groups. She wanted us in the end to brainstorm possible modifications, and I recommended that even skip-counting games like BizBuz can be modified to have students pick algebraic expressions out of a bag, show it to the class, and then say either Biz or Buz depending on whether they are divisible by either of the two expressions specified by the teacher at the start of the game. I am excited to try this game with my Grade 7s when they get to basic algebraic factorization later this year! Another game that I think is very adaptable to the MS classroom is a variation of the spelling game that she administers. Start with kids standing in a circle; one kid says a shape name, such as "Square." Then, the next ____ kids will need to state all the identifying properties of that shape. "Has 4 sides." "Opposite sides are congruent." "All angles are right angles." "All sides are congruent." "Diagonals are congruent." "Diagonals are perpendicular." When all properties have been stated, the last kid says, "Sparkles!" and does sparkly jazz hands (I'll have to see how this works out with my MSers; maybe the sparkles part is too much for them). And the next kid in the circle will get to name a different shape, and this starts over. If the "Sparkles" are prematurely called because there are properties that have been missed, then the kid who called the sparkles would sits down. If a kid says a property incorrectly, then they also sit down. Round-and-round we go to review properties of polygons....

Finally, I went to a talk on tips for school leadership, led by Paul Morris, who is an elementary principal in Stuttgart. Even though the general presentation format was not my favorite, it had some gems of advice. Specifically, these were the things that stood out to me:

• Spend more time with the people who disagree with you / dislike you than the people who like you / support you.

• If you are pushing a new initiative, you need to get a core group of supporters and then just MOVE. It's not possible to wait until everyone gets on board.
  
• Education fads come and go almost faster than shoe fashion. Get your teachers to help you decide which new trend is a fad, and which is not. Choose carefully.
  
• Consider carefully the flow of info from meeting to meeting. Design your meeting schedules in a way that pays respect to this need
  .
• Give parents credit for advocating for their child, even if they may appear misguided to you.
  
• Admit when you've made a mistake. This models for your teachers how to interact with children and each other.
  
• Understand that it is very difficult sometimes for international families to adjust to a new situation, and they take it out on the school because that is one thing that they feel they could have control over. Be patient.
  
• Consult as many people as possible before making a decision. But, don't be afraid to make the decision.
  
• If someone sends you a one-on-one email, do not write them back. Go find them in person to discuss it. Make opportunities to make face-to-face contact with your colleagues.
  
• Remember why you are here. Have compassion. Teachers and students are equally important.
  
  
• Work from different places. When you get out of your normal working place (ie. office), even if it's just taking your laptop and sitting somewhere else, you gain new perspectives.

OK - last day! And then, off to enjoy my Sunday evening. whew. 

TI-84Plus COLOR vs. TI-Nspire; Flexible Grouping

I saw a nifty little presentation today by a TI rep, showing off their latest gadget called TI-84PlusC. To me, it looks like a cross between the TI-83/84 series and the TI-Nspire in terms of functionality. It can import a photo behind the graph for modeling purposes, and it has colored lines and table values. It also allows you to turn on the grid inside the graph, in order to make it easier to estimate points. (These are all features on the TI-Nspire, but this calculator has the same familiar input buttons as the classic TI-83/84s.) The only drawback seems to be that it cannot work with ViewScreen, the piece of hardware that projects the student's calculator work to the wall. It has to do with TI not having enough customer demand for ViewScreen to make it worth it for them to make something that is compatible with the TI-84PlusC. Anyhow, the SmartView still works, and on the new SmartView software for TI-84PlusC, you can tab between the colored calculator view and the plain black-and-white calculator view, in order to support the kids who have different calculators in your class.

The new calculator costs a bit more (maybe 20 Euros more) than the old TI-84Plus, but is comparable in price to the TI-Nspires. I think this might be a viable option for us to order in bulk for our department, instead of TI-Nspires, because from my limited toying around, the TI-Nspires seem to generally require more keystrokes to perform the same function, which -- if true -- would put our kids at a slight disadvantage on timed external assessments like the IB. Anyhow, I am glad that there is an alternative to the TI-Nspire that is a compromise between the "old" and the "new" versions of TI calculators. They're due to be released I believe in March, and in April there will be special teachers' discounts available to bundle the teacher's software (SmartView) free with the calculator order. You can also get a free software upgrade if you already have SmartView currently installed on your computer for the plain TI-84.

-----------

Besides that, I also heard today about a very interesting setup at Munich International School, which has to do with a fluid leveling/grouping program that they implement in the mathematics department. There they have common teaching/planning blocks in the middle school, and they agree in advance of every math unit, what the time frame of that unit will look like and what is the common assessment they will do at the end of the unit. Then, they give all the kids a pre-test and then split them up into ability groups, FOR THAT UNIT ONLY based on their pre-test scores. The kids in the lowest group are supported by an extra teacher. (There are 4 teachers for 3 ability groups, so the 4th teacher is sort of a floater who ends up helping out with the weakest group to allow more intensive attention to be given to those kids. I think this 4th teacher is also a more senior teacher who helps to facilitate with curriculum development.) In the years that they have tried this at their elementary and middle school levels, they have really experienced a lot of success for both the top and bottom kids. The last year (and they project also this year), they were able to extract 2 honors/extended classes going into high school, instead of one. They're essentially taking the best parts of streaming (allowing weaker kids to shine, allowing stronger kids to move along) and taking away the stigma that is associated with being "stuck" in an ability group. They also don't do grouping all the time, and the kids start to be advocates of their own learning, sometimes requesting to move down for a certain topic, in order to focus more on the basic skills. There are only 3 blocks a week when the students meet in these ability groups, and for the other periods they still meet in their homerooms, so they understand that the grouping does not define their identity but merely serves a very specific purpose.

It really sounds fabulous. I think there might be some challenges with implementing it at our school, but we're still excited about bringing it back as a radical idea to discuss. I wanted to pass it along in case some of you might be interested in implementing this at your schools....

----------------

So far, the AGIS conference is going great! If only I wasn't having the allergy attack of my life, it'd be perfect.

Pencast as My Substitute

I am going away for a conference on Friday. In order to give my 12th-graders the maximum chance for success, I have tried to create pencasts for all the problems in their packet, so that they can try them (hopefully really try them, OMG senioritis!), and then the substitute will just hit Play to go over the answers.

Like this one.

I am really impressed that PDF has the built in feature to support animations and wav files. wow. Yay to a hopefully still productive day in my absence. Yay to our new Livescribe toy, from which I can see many possibilities for the kids who just need a little more TLC...

Perpendicular Slopes and Geoboards

I'm delving back into the nitty-gritty linear concepts with my 8th-graders. I came up with an idea of teaching perpendicular slopes using Geoboards. I haven't tried it out yet, but I think it's going to work. They can first try and build a right-side-up square on the Geoboard and draw it in their notebooks on graph paper. Introduce the term perpendicular. When you ask them to draw it on their graph paper, remind them that when we look at shapes and their side lengths, we're counting space units along the side, and not the number of pegs. Then, the plan is to switch it up:

Challenge them now to build a diagonal square in the geoboard. Have them discuss when they think they have found one. Ask them to draw it on their graph paper. And then, once they've found/drawn in their notebooks a bunch of different diagonal square examples, have them look for commonalities. If I now put just one rubberband or segment down to represent one side of the square, can you find out exactly where its perpendicular side needs to extend from/to? What are their slope values? Is there a pattern? Use this to lead in to the idea of reciprocal slopes with opposite signs.

I like this activity idea, because potentially, if it works, you don't have to teach the kids the "negative reciprocal" idea like they are robots. I'll try it this week and then report back. Maybe we'll even have some photos! (I need to keep reminding myself that I need to start accumulating photos of my homeroom kids, for the yearbook.)

And, anyhow, I am excited about my first Geoboard lesson of the year!!! There's nothing quite like handing rubber bands over to 8th graders and expecting them to put them to serious use. :)

Kid Writing Samples: Round 1

I talk regularly about how I think that kids must, and I mean MUST, write in the math class. It's a lot of work for you as a teacher because you need to give time to do something lengthy, and then give some time for them to start the write-ups during class, then you need to give them copious written feedback on the first draft, and then maybe have a discussion with the whole class about how to organize their ideas logically, and then you need to still read every kid's final draft and to assign them grades, and then to post a task-specific rubric. In the end, this process is so SO worth it, even if some of the kids' products are not stellar. The important thing is that when they write, they are really learning about what it takes to put their mathematical thoughts down in words in a way that makes sense to another person outside of our class, and they're forced to re-evaluate how well they themselves understand each step. Moreover, if they are asked to make a draft and then a heavily revised draft, they begin to invest in the quality of their work and to learn to take pride in their work -- no matter how much help they might have needed along the way.

Here and here are two lab write-ups from earlier this semester (maybe November), when the kids wrote about the process of stacking cups to match a classmate's height. The two kids I posted are just two random kid athletes who happened to send me their files before they went away on a sports trip, so they definitely weren't the most polished pieces from the class, but they ARE a realistic look at what "regular" 8th-graders can do with a bit of support. (These have some errors in them, of course, but I decided to just post them as is. The kids who had really top-notch, exemplary projects didn't submit digitally, and I haven't bothered to scan them.)

I also have some interesting samples of the percent/shopping projects and the three-variable projects that my 7th- and 8th-graders worked on at the end of Semester 1, leading into Semester 2. I'll post those in a few days if you check back then. They've turned in their "first drafts", which they think are polished (last graded assignment of Semester 1), but look fairly hairy to me still, and now they'll get a chance to polish those drafts based on my written feedback, for the next round of submissions (counted as part of Semester 2).

Hope this makes you excited about writing in the math class! I love projects and I love making kids write about math. For me, I think all worthwhile math projects are inherently interdisciplinary, because even if you're teaching strictly math, as soon as the kids are asked to communicate, reflect, present, create... then you're already bringing in essential skills that they develop from other classes and helping them see that other subject skills do not stop at the classroom door. After all, we are full-time educators as much as we are math teachers. :)

PS. I have to admit that sometimes, grading the first math writing assignments of the year makes me very aggravated, because most of the kids have never done such math tasks before my class. They don't know how or when to use diagrams to visualize; they jump straight into math discussions without any introduction; they either write a lot of symbols without attaching any description OR they just give numerical results without showing the work on how they got those values; they keep repeating themselves because they cannot organize their thoughts in an efficient manner; and they seem to have developed some secret language that doesn't make sense to anyone outside of the class but me, in describing their mathematical process. But, THAT IS EVEN MORE REASON for them to write!!! By the time they leave my class, I would say that the majority of students can piece together a fairly coherent discussion of a relatively straight-forward math topic, without too much help on my part.

I just wanted to put this out there in case you are wondering, "Is it just my students who are so bad with mathematical writing?!" The answer is No. Usually I have to eat a lot of chocolate and to take lots of rest breaks when I grade the first writing assignment "rough drafts" of the year.

Big Life Change.........?

Since I've talked to my admin, now it's OK for me to say it to you guys: I will probably have to move at the end of this school year, sadly.

I love LOVE my current school. I will be sad to move. But, a potentially great opportunity has come up for Geoff, and for that we would have to relocate back to the U.S. It is something that I couldn't ask him to give up, so I decided that I loved him more than enough to give up what I have here and to take a leap of faith. So, I told my school this week that although I am still waiting for more clarity on his part to fully decide, I wanted to let them know of this probability of leaving, so that if they felt the need to immediately start looking for a teacher, they could do that and not lose out on the chance to interview quality math teachers. I was very nervous before telling them, because I didn't know whether they would understand my priorities and whether they would be supportive. To my relief, they were super understanding. They said they will wait for my final decision before looking for a replacement, because they'd much rather keep me than to hire "anyone else." Awwwwwwww.... That is so-so-sooooo sweet, but it also makes it hard to really come to a happy, final decision. (I almost would rather them say that they will start looking tomorrow for a replacement, so that I'd be forced to find a job.) Anyhow, so I decided that I'll be looking in Seattle for a teaching post during my February visit, and either I'll find a job that I'm excited about, which'll firm up my decision to move, or I'll see/visit schools that may not be immediately hiring but are promising opportunities, which'll also help to make my decision to move, or -- if nothing looks right and Geoff's job situation is still muddy -- we could decide to stay in Berlin. We will then let my school know, immediately following our February break, so that they can start interviewing if they need to. And, they're totally OK with that timeline! (I have the best admin, seriously. They've always been incredibly supportive of me, in things big and small.)

So, although I am very sad about potentially/"probably" leaving my school and my job as department chair (I was really just starting to feel like what I do makes a difference to the teachers), I have to ask you to keep your ears open for possible openings in the Seattle area. I promise you that I'm great to work with, even though you guys have never met me. Here is my CV, and a cover letter as well. Let me know if you know someone who knows someone who knows someone in Seattle... Help a sista out!! xoxo.

Request for Resources on Benefits of Technology

Hi everyone,

I am searching currently for any resources (printed or web) that you can point me at, that discuss the benefits of graphing calculator-based learning of mathematics. Within our department there are some differing opinions about this (since some teachers are still quite traditional), and so a colleague has asked me for more resources so that they can further analyze this issue. I thought I'd ask you guys, who are the experts, to see if you had such resources handy. Personally, I feel that technological approaches in general can help students visualize math in a way that helps them to understand connections between graphs and algebra, which was not possible a generation ago for the kids who lacked fluent graphing skills. It also serves as a motivation, as you can already see the desired end result and you're just working towards understanding the process to getting that end value. It also helps with problem-solving, in bypassing the hump of algebra, since in the "real world" they may not remember how to crank through every problem manually but they'll still need the analytical skills to be able to evaluate a graph and what it means. BUT, that's all just what I think. What "official" resources or studies do you have that can corroborate this?

THANK YOU!

Visual pattern of 3 variables

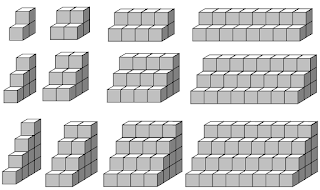
Since I have multi-input relationships on my mind, here is a visual pattern of 3 variables for you to enjoy (row, column, result). I've submitted this to the good folks at visualpatterns.org, but because of the nature of the complexity of this problem, I'm not quite sure that it quite fits well with everything else over there. Anyhow, it's a good problem for your abstract thinkers and ties in the concept of both arithmetic and geometric sequences quite nicely, I think.

Above shows rows 1, 2, 3 starting at the top. It also shows columns 1, 2, 3, 4 starting from the left to the right. At this rate, in row 8, column 10, there will be 23040 cubes. Can you find out how many cubes there will be for row 20, column 15?

Wedding Excitement

OMG, I get married in less than 90 days, and I cannot wait! The dress fiasco got fixed, eventually, by my wonderful seamstress. I think altogether we had about 5 or 6 fittings, but it was totally worth it because in the end, the finished product was unique and very appropriate for a beach wedding! (I took a dress on the rack that I had liked but that was a lot of sizes too big, essentially had them take it apart and remake the dress to fit me, and then they had to create fabric to simulate the dress in order to alter its style, and then I had a whole other part made to be added to the dress.) During the entire process, my seamstress was wonderfully patient, and in the end she almost didn't accept my extra tips for her!! (She said, "That is my job!") If you live in Berlin and you're thinking about shopping for a wedding dress, and you think you might want something altered and not directly off the rack, I highly recommend Crusz, the abendkleid and brautkleid shop near Spittelmarkt. You will be very happy with Alex, their on-site seamstress!

And then today I went accessories shopping. I needed shoes, some hair decoration, and a necklace. I decided to head to Charlottenburg, because that area of town is relatively nearby (it was snowing hard today) and also it's pretty posh, which means that it has the potential to have nice accessories. In the end, I bought a very simple single-pearl necklace (for me, since I don't have very sharp facial features, sometimes simpler is better because then it does not overwhelm my look) en route to one of the shops, Felicita, which I had found online. When I arrived at Felicita, I noticed right away that 1. They have vintage-inspired dresses and accessories, which is awesome because I dance swing so I like vintage things, 2. The shop-owner looks familiar. I think I had been there before when I dress-shopped, but the dresses they showed me didn't quite have the "wow" factor for my face/body type. (They looked beautiful and vintage and romantic on the rack today, so I'm pretty sure it's just a misfit for my style.) Anyway, I wasn't sure what I wanted to find there, but I had brought along a fabric sample from my dress, so I showed it to them, as well as a picture of my dress (which they said is a very "modern" style... I think they were surprised by it), and they let me try on a few hair accessories that they thought would work well with the dress. (Because it was "modern", they had immediately rejected the idea of a veil. Good thing, since I had already rejected having a veil based on the possibility of a very windy day on the beach.) And, they were right! The first hair thing that they brought me was not something I would have picked out for myself, but I absolutely loved how it looked on me/how it complemented my necklace, and immediately I could picture it going well with my dress as well. They ended up showing me a few others, but that first hair accessory was still my favorite, so I did not hesitate to buy it.

Then I tried on some shoes there, and they had some nice, simple, comfortable, and even vintage-inspired shoes. But in the end I didn't feel confident making a choice without trying the shoes on with my dress, so we agreed that the next weekend I'll go back, bring my dress along, and give it another shot. Hopefully I'll get something then, so that this won't be a "thing" hanging over my head as we move into February...

--But, in any case, I am still miles ahead of Geoff, who hasn't even started to think about what he's going to wear at our wedding! I am not really worried though. I had looked through the wedding photos of our wedding planner's past events, and most of the guys dress very casually, and they still look good on the beach! I'm not stressed. I think Geoff can wear khakis and a hippie shirt, and he'd probably still be fine.

Anyway, now that my attire is slowly coming together, I am very excited about the wedding!! We have about 50 guests, I estimate. The girl at the shop mentioned that this is like a dream wedding, and it is!! I am starting to get totally excited about my wedding, even though I had never thought about weddings until about a year and a half ago.(I'm not one of those people who dreamed always of weddings. Actually, Geoff and I aren't even having a wedding party, just to keep things simple. We would have been very happy to get married even with just our parents there! Having 50 guests, many of whom are staying at the same resort as us, is like a dream. And since I'm going to ask ALL the girls to wear flowers in their hair, it's going to be very festive and lovely all around, and it'll also help everyone feel extra lovely!)

So, yeah, this is probably my last wedding update before the wedding. (I hope.) I'm going to take this opportunity to say that it's a non-zero possibility that there will be math puzzles at my wedding, since Geoff was pretty enthusiastic about the idea. I think it's "only right" that everyone completes a puzzle before they can get their first drink, and it'll also help people mingle to help each other. :)

Grade 7 Project: Percents and Shopping

Speaking of projects, I recently had a very lovely experience collaborating off of my colleague's percents project. I took an old project that she had written up and added extra components to it, and then gave the feedback back to her so that in the future she might incorporate the new elements. I really loved this iterative process, and she was happy as well!

Here was her original project.
Here was my add-on.

Essentially, I took the same percentage discount elements (my kids are still calculating percents by dividing by 10 to get 10%, and then working through proportional reasoning) and then added a creative component, where percent increase (shipping fee) was incorporated into this project by asking the students to come up with their own online shopping story. I also would only check the first two steps (1A and 1B) of the project, plus the calculations for their individual creative piece. The rest of the project had to be checked some other way, so they had to brainstorm ways to check their work -- and they'll be graded on this "reflective" process in addition to their overall explanations, clarity of thought/work, and accuracy.

In the end, the kids helped each other to identify a variety of math concepts (decimals, rounding, percentage, addition vs. subtraction, sequential application of percentage change, checking your work using inverse operations) that were required in this project. I'm still waiting for their writeup, to be due next week, and then probably a revised version (depending on how well the drafts are done the first time). I'm quite happy about how it has gone thus far!

These same 7th-graders also rocked their algebra, fractions, and basic percents on the first semester test. They had come in to my class not knowing integers, order of operations, or how to calculate even simple fractions. I'm so proud that they ended up doing better on the semester exam than my previous students did a year ago!!! WAY TO GO, GRADE 7. Rocking my world, one day at a time.

3-Variable Project Success!

This is a follow up to my three-variable project in Grade 8, which we're finally doing now that the semester test is out of the way. The kids are really enjoying it, and it helps to solidify the idea that multiple variables can cause the numerical output to change. (I tied this in our introductory discussion to familiar formulas like A=lw and P=2l + 2w). Prior to starting the project, I also quickly pulled up a real-world 3-variable table and asked them to tell me where the causes are and where the effects are, inside this format of the stockings sizing chart. This really helped them to understand and relate to the table setup on their given project sheet, in terms of visualizing why the table is set up that way.

They worked through the first table with guidance, and found the general formula pretty easily once I asked them "if n = 100, what is the formula for y? What if n = 372? What if n is just any n?" After this, they repeated the process for the second (and for some students, as well the third) table of values. The last two days we worked on verifying the general formulas they found, first manually -- learning to show proper work for multiple math test cases -- then with technology.

It took me a little bit to figure out how to set this up, but I made this http://bit.ly/excelTestTemplate to help my 8th-graders test their general formulas for their projects. I am very excited to see the outcome of this project, because as part of the testing procedure I also taught them how to program a very basic loop in the graphing calculator, in order to prompt for two variables, perform a basic formula, and then output the results. It looks like this for testing the first formula y = mn + n.

:While 1
:Prompt M
:Prompt N
:Disp M*N + N
:End

The kids took about 30 minutes today programming their graphing calcs to run their general formulas, testing them with a few entries from the table, and documenting it all using their camera phones in order to insert it into the math reports that they will be working all of next week. SWEETNESS. This'll be their second time writing a formal Grade 8 math paper for me, and since the first ones were pretty decent, I think this round will be as well.

I also made this project writeup guidelines to help them with framing their writeup. We discussed at various points of this project, how this mathematical process is very similar to the scientific process, with looking at the effect of a single variable at a time, then combining results to form a general hypothesis (ie. the general formula involving all variables), then test-test-testing your hypothesis using a variety of test cases and test methods. What a perfect age group to do this with, since their little minds are just opening up to the world of thinking logically and sequentially and doubting everything.

I hope you have a break in between heavy-duty algebra topics to do this with your kids. Highly recommended! Super duper multi-faceted project involving a variety of skills.

Addendum: My colleague recommended to me that at the end of the project, I show the kids  the 3-D graph using x, y, z as the variables. Wow, that's pretty crazy. I don't know if they're quite ready to handle this!

My New Year's Resolution!

I have a feeling that 2013 is going to be insanely busy, but still, I think I am going to use my free time towards a cause that I think is worthwhile. I think there are too many great math lesson resources out there on the web, but they're all scattered all over the place and not organized in a centralized location. I know that when I sit down in front of the computer, usually I only have a few hours to plan a lot of lessons. That makes cross-checking all of our wonderful sites for all the possible lesson resources, a nearly impossible task. So, for myself and hopefully for some of you out there, I'm starting a teacher-friendly repository of Common Core Math Lessons !

I think/know I have seen some of these attempts at collecting CCSS lessons out there, and yet when I tried to click through the repositories I could find from google, there were lots of nested links that led me to a dead-end page. That's got to be one of the most frustrating designs ever! So, I decided to make this wiki structure very flat. You go from the landing page via one click to content listed by grades (some of them are mixed because there is some overlapping content between grades, or just because I think it's more useful to list progressing content side-by-side so you can see the link to previous/next grade level), and then the links to lesson material are then visible directly under the topic overview.

I am going to spend my own time working on this, starting with grades 1 through 5. (I've already more or less fleshed out grades 1 and 2, using lesson material that I found on the web since I've never taught those grades myself.) I would really love it if this could be a collaborative effort! I think of it as an interactive textbook of sorts, or lesson plan book, that steps through some effective methods of teaching math topics as outlined by the Common Core. If you feel that there are lessons you already know (whether your own or someone else's) that would fit nicely into one of the existing topics under the Common Core, then please contact me and I'll add you to the list of editors on the site!

Thanks a bunch, and happy jolly 2013! 

Thinking About Investments

A girl I went to high school with (Shereen) is entrepreneurial and she recently produced this frankly, pretty badass video interviewing another female entrepreneur. They have some pretty great advice (especially towards the end of the video) that I think is good for people who are thinking about doing something they love, related to their interest, and getting out of working for the corporate ladder.

One thing about this interview that immediately piqued my interest was when the interviewee mentioned the book Rich Dad, Poor Dad, which if you haven't read it yet -- please immediately run out and purchase it! Even if you are not able to put those concepts into use immediately, it's mind-opening to think about ways to leverage money to work for you, rather than you working for money all the time. Geoff was the person who had introduced me to this book, because he says that it aligns closely with his own investment philosophies. He also thinks that in general (and especially in Berlin), people our age do not talk enough about investment -- they're still on the mindset that the government will take care of us when we get old, which in the case of Americans, is simply not true (and I think the German socialist system will as well hit problems down the road). And when they do talk about investments, unfortunately for the most part, they're thinking in the wrong frame of mind about it.

Here is an example of the mindset difference:

My parents were incredible savers. They each worked in Taiwan for airlines for about 15 to 20 years, and bought a condo with their savings. When they sold the condo and moved to the States with my sis and me, they were about 40 years old and my parents put a cash down for $180,000 on our house. That's really incredible, because I doubt that in 10 years, at the moderate rate that I am saving (and I earn substantially more than they did), I'd have half of that cash, saved properly in the bank, to throw down on a house.

When I told this story to Geoff (who is very entrepreneurial and has been working for himself since he graduated from college... the road has not always been smooth, but even so, he wouldn't trade it for the world!), Geoff's response was that he would have tried to seek out as many loans as possible, and then leveraged that $180,000 to buy a two- or three- family unit house. Because if you crunch the numbers and make reasonable estimates of rental income, it is possible to rent out the remainder units and then to use that to cover most of the mortgage, so that essentially your living cost is free. Risky, yes, but that's what Rich Dad, Poor Dad recommends and that is what Geoff's always on the look out for when he makes his own investments -- finding ways to leverage his money, so that the investments bring in profits every month instead of him throwing more money into the investment every month. In fact, the whole premise of Rich Dad, Poor Dad can be summed up in saying that regardless of your day job, it's what you do with the money that you save that will really have a long-term impact on your income. And that is still a radical mindset shift, even for me as I hear Geoff talk about his strategies. Geoff's whole philosophy is that if you diversify, you would have some riskier investments that bring in higher profits, and then some safer investments that bring in minimal profits -- but note, none that would cost you money in the long run! -- and then if you accumulate the profits over time and re-invest them in other things, then sooner rather than later, you are making enough monthly investment income to gain financial independence. And that is the take-home message of Rich Dad, Poor Dad. In the end, if you invest properly, you should be free to work on anything that you choose and not be bound by whether you are making money, because simply the investments you have made could be generating enough income to sustain your living. (It's not that easy to do, obviously, because you have to be willing to risk your life-long savings, and you have to really do a lot of market research before plunging into any investment -- the first time Geoff bought a piece of high-risk property in Newark, he had gone around and looked at over 100 houses beforehand! He trained himself to become an expert at looking at the potential of a place and to crunch numbers to minimize risk of loss. But, if ever you were to make such risky investments, it's now when you're young and you can still recover from the losses...)

Instead of leveraging their money the way that Geoff would have done, what my parents did was the traditional American thing: They put down $180,000 on the house, bought a house that was worth $300,000, and then were drowning in mortgage payments until the housing bubble, at the peak of which they sold their house for double the price they had purchased it for and retired on that profit. Essentially, my parents got lucky (and my mom cannot stop being thankful for this), but our generation -- we can do better. And we can do so without changing our day jobs -- we can still be the teachers that we are, but become smarter with what we do with the money that we have saved.

I thought I'd throw it out there in case you have not yet come across this amazing book, Rich Dad, Poor Dad, which is every bit as impactful as the girl describes it in her video interview. I think it's a must-read for everyone in their 20s and 30s, right now, who lives in America, and (for those of you who don't already love your jobs) the girl being interviewed also makes a great point about starting off small, and how to apply that idea of ownership to something of your own interest!