Estimation of Circular Areas

It's my first time teaching circle formulas. Teaching circumference was easy: First, we went around the room and measured a bunch of circular objects, recording both their diameters and circumferences. Then, we put the values on the board in a table and calculated the ratios between the measurements ("how many times bigger?") and observed that it was always just over 3. Then, we practiced estimating circumferences given diameters. Then the kids learned that the exact ratio is pi, and they practiced finding circumferences, both exact (in terms of pi) and calculator approximations, when a diagram shows them only the radius.

Then... I gave them this. It's probably not special, but it worked well for us!

Questions I asked (on a worksheet, so each kid had thinking space and doodling room):

1. What is the area of the shaded square?
2. What is the approximate area of the 1/4 slice of the circle? How did you get this?
3. What is the approximate area of the whole circle? How did you get this?

After individual attempts and a brief whole-class discussion, they then practiced estimating areas of various other circles using the same technique. (On their paper, again, so they can each think at their own paces.)

We have not yet discussed the circle area formula. I am insistent on this. Area formula has to come after estimation, so that they can remember why it makes sense that (3/4 * r^2)(4 slices) leaves you with a circular area of approximately 3*r^2, or pi*r^2 to be exact.

Yay 7th-graders for being good sports and being open to a world where we develop formulas together!

Pop-Up Math Book Project

In addition to doing the end-of-year creative assignment in Grade 8*, I decided that Grades 7 and 9 will do a pop-up math book for me in June as their end-of-year assignment. It's not graded really; it's just for them to have something over the summer and next year that they can look back on to remember how we approached the concepts and how they individually understood them. They are encouraged to make it very colorful and creative, a la foldables, so that they would be inclined to come back in the future to use it. There is a lot of writing involved in this project, so they will be forced to revisit all the concepts and to articulate them in their own words.

Here is a link to the specs that I made for Grade 9 (this is a slower-paced group, so many topics may seem easy for the age group). I also made a sample booklet with some pockets and flaps and tabs (but it's only a template and has no content), so that I can have something to show them of what I am envisioning and what are some formatting options they could try for the different pages.

Excited! I've never done this project before. That can only mean good things. :) :) In fact, as their "choice" assignments, a few of my Grade 8 students wish to do this pop-up book as well. It has the potential to be fabulous.

*Um, by the way, I think one of my Grade 8 groups is going to build me a trebuchet and then do some math predictions / modeling on that thing. I am thrilled, because they told me I can keep the trebuchet afterwards!

Addendum June 21, 2012: Here is the follow-up link, with links to photos of some finished projects!

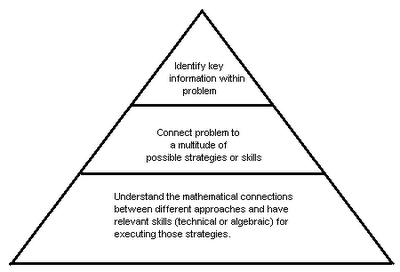
Problem-Solving Pyramid

I think that this diagram represents my current analysis of the separate layers of skills required in order for a student to successfully solve a problem that involves some not clearly named algebra skills.

In class, I think I work on the bottom layer a lot, and I only periodically go over strategies and cues from problems. I think I overly rely on my students to work on the top two layers on their own (falsely deemed "intuition"), which is unrealistic and is contributing to their not-so-great mock exam scores. Now that I have in my head a visual representation of these various skills, maybe I can better communicate it to my students and emphasize strategies for building each layer. I made the diagram in a pyramid form because I think the bottom layer is more broad, as in it can later be applied to a variety of situations and problems, versus the top layer is specific to the problem you are looking at / working with.

What do you think? Do you agree with this mental model? Do you think it helps to clarify strategies for teaching problem-solving? (Do you think it's "obvious"? Sorry, but the obvious things are usually unfortunately either not obvious to me, or they're so obvious that I don't really execute them effectively because I just don't see them. sigh)

Completing the Square Geometrically

I am so excited! I taught completing the square today in my "low" grade 9 class for the first time, and I decided to try a geometric approach this time as inspired by my friend from PCMI (the awesome Danielle Soderberg*), and the kids loved it!! After just two examples on the board, they had no trouble at all working through cases with integer leading coefficients and integer vertices. It was fantastic.

Here was the worksheet I made for completing the square, and here was the warmup sheet I used prior to introducing complete the square (cut into half-sheet strips; the kids skipped the conversion to vertex form at the beginning of class and came back to that column at the end, after the lesson).

Enjoy!

*Although, as a small disclaimer, I never saw Danielle's worksheets, so it's quite possible her approach is different and/or it is far superior. She vaguely mentioned something about algebra tiles and completing the square.

Fostering Creativity

I have just finished reading a book called Imagine: How Creativity Works (Amazon link), and it was very inspiring! The book's big message is that creativity is not a natural trait nor a momentary spark but something that we can cultivate and sustain -- in ourselves individually, in our organizations collectively, and in our communities if we make the right kinds of investment.

The book traces the success of some continuously innovative companies such as 3M and Pixar, to introduce what systems they have put in place in order to foster continuous innovation. At 3M -- the company that invented Post-Its and masking tape, among other things -- their big thing is to encourage employees to spend 15% of time per week tinkering with new ideas, as long as they report back their findings. They also encourage flexible schedule and let their employees take random walks or breaks from solving a problem, since they believe that exposure to new situations helps you draw connections to existing problems you're working on. At Pixar, physical proximity is key. They put all the people in the same building and all the bathrooms in the same area, so that you're constantly running into people you know and having random conversations. The best solutions, they say, come from these random collisions. Pixar also values group critiquing sessions followed by productive suggestions -- they call this plussing -- because Pixar believes that this surfaces issues that everyone can think about, learn from, and try to solve long after the meeting is over. A great quote from this part of the book to illustrate Pixar's emphasis on relationships is this: "A mediocre team will screw up a good idea. But if you give a mediocre idea to a great team and let them work together, they'll find a way to succeed."

If you are leading a group of people, the best type of combination is to have some people who already are well-connected to each other, as well as a healthy influx of new people with new ideas. When they studied Broadway musicals, this mix of old and new relationships among the creators of a musical had a high correlation to the commercial success of the musical. Certainly, this makes me think about my department and how we can best utilize the combination of teachers we have...

The book also touched upon the issue of fostering creativity in education. My biggest takeaway in reading this section is that when they interviewed people in charge of an elaborate art program where students learn to create things through hands-on apprenticeship/extended projects, the director said that even though they realize that most of their students will not become artists in those fields, what they leave with is a recognition that creativity takes hard work. "Because they spend five hours every day working on their own creations, they learn what it takes to get good at something, to struggle and fail and try again. They figure out how to dissect difficult problems and cope with criticism." As an educator, it makes me wonder what types of long-term challenges we are offering our students, in order to foster these qualities.
 
In terms of what you can do individually to improve your own (sustained) creativity, the book highlights the importance of continuously thinking "like an outsider." It points to the benefits of being immersed in a foreign culture, because that type of experience increases your ability to observe ambiguities and to see the possibility of interpreting the same thing in multiple ways. Based on the cited research, people who have lived abroad in a different culture tend to be better at solving certain types of lateral-thinking puzzles. But, even if you only tell people that a certain puzzle comes from a different, exotic place (like India), automatically their ability to think outside the box increases and they can solve the puzzles with more ease by thinking of less obvious interpretations and alternatives. What this means is that we have control over our ability to think outside of the box in a non-linear fashion. We need to always imagine ourselves as a brand new person who has never had any proper training, in order to allow for greater possibilities in approaching a problem. For me, this affirms my experience that whenever I move from place to place, the new challenges that come from teaching a new population and working with new colleagues and new constraints push me to re-examine everything that I do and to try new approaches. Next year, I look forward to the possibility of taking on an intern teacher, because they will come with fresh eyes, and I hope they could show me new ways of questioning what I do.

One last thing that the book continuously emphasizes is that frustration always precedes innovation. If you find yourself stuck in a challenging situation, try to see it as an opportunity for trying something new. I really liked this quote: "FAIL BIG!" It parallels my belief that a good project should run until its wheels are falling off.

So, I said that I feel inspired by this book. These are my personal takeaways:

I hope that as a teacher I will always be curious and to look to grow.
I hope that I can be continuously creative, through the network of people I have, my own interests outside of class, and through taking on new challenges.
I hope that I will have the opportunity to foster a team whose teamwork can lead to innovation.
And of course, I hope that at some point, our schools can all institute creative projects that teach kids the value of innovating through hard work!

Good vs. Great?

This is a "help me!" post. I am currently away chaperoning Grade 8 kiddies in Prague during our annual school-wide trip week, so there's not much to report in the teaching department.  But, something has been on my mind and so I am posing it here to see what you think and whether you can point me at specific resources in your links archive...

What makes someone a good teacher, and what makes someone a great teacher?

I am looking for articles or videos or other resources to help me inspire teachers who have already been teaching for more than 10 years. Thanks!!!

Addendum May 12, 2012: Here is a nice little link. The best part is the first paragraph, which is written by Thomas Cronin in The Journal on Excellence in College Teaching (1992).

Great teachers give us a sense not only of who they are, but more important, of who we are, and who we might become. They unlock our energies, our imaginations, and our minds. Effective teachers pose compelling questions, explain options, teach us to reason, suggest possible directions, and urge us on. The best teachers, like the best leaders, have an uncanny ability to step outside themselves and become liberating forces in our lives.

Great teachers know that they are always on stage and that who they are, how they act, and what they believe are as important as what they teach. 

Mini PD Topics for Next Year

I am slowly brainstorming mini PD topics for next year for my department. (Actually I've already been thinking about this on and off, but I am writing them down here to start a written record of some sort.) I know I will have to tread lightly as the new chair, but I think it's important to introduce some shared language into our department for discussing pedagogy and learning strategies. About once a month, I would like to highlight a single topic and to bring in resources to share with the department, to discuss what we are already doing vs. what other things / realistic changes are possible.

1. Habits of Mind - how do we teach/assess these?
2. Scaffolding vs. productive struggle
3. How do we teach for retention?
4. Motivational techniques, "hooks" for lessons, and two-week rhythm
5. Conceptual vs. skills development -- false dichotomy
6. What makes a good problem?
7. What makes a good project?
8. Long-term "backwards" planning vs. hinge points in individual lessons
9. Examining scope and sequence more closely - how are concepts related, why do we teach things in this order, and can we do better?
10. Meaningful adaptation of technology

Other ideas?? What big topics am I missing in helping already experienced teachers examine their own practice critically? Once I decide on a rough list of topics, I would appreciate any help you can give me in providing thorough and/or very clear resources that discuss each of these topics. THANK YOU! :)

Wow!

I found out today that I will be the head of my department next year! yay! Although I had really hoped this would happen (I had submitted an application letter last week detailing my visions for my role as the HoD, and I had to shrink the margins in order to make everything fit on one page), this result still came as a real shock. I am probably the youngest and definitely one of the least experienced teachers in my 9-people department, and besides the new part-time math teacher who will be joining us in the fall, I will be the only non-tenured staffer in my department. (Many of my colleagues have had years of teaching experience.) When I think about the challenge of leading a senior department such as ours, I am truly humbled. I have NO illusion that it will be easy, but I am prepared to do my absolute best.

You know what this means: I'll be looking for pedagogical resources to share with my colleagues, because it will take a lot more than enthusiasm to do a good job. My goal is to help my colleagues to appreciate each other's expertise and to encourage them to incorporate new teaching methods into their own classrooms based on educational research and their students' feedback. I would love your help and pointers as the year progresses.

I know it's too early to celebrate (until I am able to make a positive difference), but... yay!! for this truly fantastic opportunity.

PS. Just to clarify, this still means I'll be teaching a full load. Either 5 grades (grades 7, 8, 10, 11, and 12) or 4 grades with middle-school homeroom. I may even get a student teacher in there somewhere. So, there is small likelihood of me sitting around...

Visualizing Areas

I recently created these for my 7th-graders to do/try individually on quizzlets. The task is to find the area for each of these shapes. I thought I'd share them here, since sometimes it's hard to find problems with the right level of difficulty in textbooks and stuff. After some hands-on play with geometry ideas and formulas, I was mostly interested in the kids being able to categorize/visualize objects and their relationship to one another.

(Even though they're familiar with trapezoids -- which, by the way, the Europeans call trapeeeeezia, or trapeeeeezium in singular form -- by now, this one below tripped many of them up because the diagonal lines don't "look" parallel. We had to discuss afterwards about what happens when you are walking along a street, make a 90-degree right turn, and then another 90-degree right turn. Are you walking parallel to the original street?)

I was pleased that they did very well on the two below, since these shapes are a bit less standard. On the quizzlet, they had to both find the area and explain the process. Go 7th-graders!

An Easy Group Game Format

When I was in grad school I learned a fun/easy math game format (from one of the best math ed professors ever!). I was reminded of this today as I brainstormed ways to review DEATHLY BORING algebra concepts for the upcoming end-of-year exams.

Step 1 (Pre-class prep): Generate two lists of numbers.
List A: 10, 14, 3, 20, 9
List B: 6, 5, 8, 12, 33, 7

Step 2 (Still pre-class prep): Make a 4-by-4 grid of numbers on a poster:

Step 3 (When the kiddies arrive): Divide up the class into two teams. The game is basic Tic-Tac-Toe (4 in a row wins), and the teams alternate turns, but in order to "win" a space during their turn, the group has to correctly make a math statement combining an element from List A with another from List B. You can customize the type of mathematical statement to the content you are currently learning/reviewing. For example, using the lists and the grid above with 6th-graders, a kid might say: "The Least Common Multiple of 9 (from List A) and 33 (from List B) is 99." In saying so, their team gets to put down their marker on the space in the grid where 99 is.

As you can see, the content is very customizable. As I shared with another teacher today, you can easily alter the content to review conversion from fractions to percents and decimals, for instance. (List A: numerators; List B: denominators...) Same goes for integer operations.

I am going to try using this to review DEATHLY BORING algebra "expansion" skills in Grade 7, along with modified Bingo* and other games I manage to think up. What types of fun things do you have up your sleeves for reviewing at the end of the year?

*We did algebra Bingo today for expanding/simplifying and then I spontaneously decided to modify it. Since kids are always trying to influence the next numbers being called during Bingo, I periodically put up "challenge" problems on the board and said that the first kid to correctly (raise their hand and) expand and simplify everything gets to CHOOSE the next Bingo number. The crowd went wild for this! The good news: Everybody was trying those challenge problems. The bad news: My 7th-graders really still need to practice expanding expressions like 0.5(x - 10)^2 and -0.5(x - 8)^2. Eeesh.

Spring in Berlin

Yesterday was a very "Berlin" day! I think there is nowhere in the world I would rather be than in Berlin, right at this moment. The air is warm and the days are long. People pour onto the streets the way people in cold regions do, when the long winter is finally over. The city awakens in a soft blanket of green foliage, and because the buildings here are not so tall, there is sunshine everywhere. In Berlin, every restaurant has tables outside, and the streets are teeming with pedestrians until 10pm.

Geoff and I biked down to Mehringdamm and had dinner on the bustling Bergmannstrasse. When we were there, we saw a piano player on an old piano in the middle of the sidewalk. A glass of wine sat on top of his old wooden piano. A German toddler wearing plaids watched on, while her dad stood by holding a bike, enjoying the open-air music. We got ice cream before dinner, because it was that kind of temperature. Even though spring has just arrived, I am sure we are already on the cusp of summer.

After dinner, we rode up the street to meet some friends at a biergarten. It was utterly lovely, and the place was just filling up as we were leaving after 9pm. I had two full glasses of wine plus a bit more, which is a bit much for me on any day. I swayed on home happily on my bike and didn't realize we were so close to home until we turned onto our cobblestoned street.

I would write a poem to describe the loveliness of summer in Berlin, but I am not a poet. I would take a picture, except it would do the city no justice. I have always enjoyed the cities in which I live, but I love Berlin like I haven't loved a place in a long time.