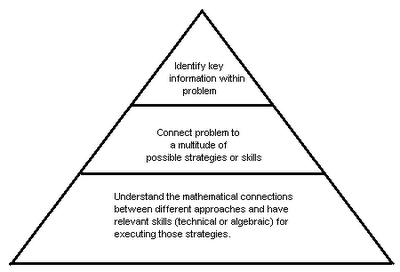
In class, I think I work on the bottom layer a lot, and I only periodically go over strategies and cues from problems. I think I overly rely on my students to work on the top two layers on their own (falsely deemed "intuition"), which is unrealistic and is contributing to their not-so-great mock exam scores. Now that I have in my head a visual representation of these various skills, maybe I can better communicate it to my students and emphasize strategies for building each layer. I made the diagram in a pyramid form because I think the bottom layer is more broad, as in it can later be applied to a variety of situations and problems, versus the top layer is specific to the problem you are looking at / working with.
What do you think? Do you agree with this mental model? Do you think it helps to clarify strategies for teaching problem-solving? (Do you think it's "obvious"? Sorry, but the obvious things are usually unfortunately either not obvious to me, or they're so obvious that I don't really execute them effectively because I just don't see them. sigh)
It doesn't work for me (yet), but I am just loving how we can throw our ideas out to each other when we have them, and get feedback that helps us build.
ReplyDeleteOne reason it doesn't do much for me is that I'm not very visual this way. Also, I don't see what each level means, really.
Clarification on the diagram:
ReplyDeleteFor example, using trig (and an old trig IB problem) as an example, the BOTTOM layer would be when I teach in class the basic meanings of sin/cos/tan, go over the connection to the unit circle and rotation, and meaning of coefficients in the wave equation. The kids, if they wish, can practice basic problems out of the textbook to reinforce these "basic" concepts and learn to complete straight-forward one- or two- step problems.
The TOP layer (problem-specific skills) would be when students read about a rollercoaster problem and realize immediately about its cyclical nature. No wave is mentioned in the problem, but they are given a table of values (time vs. height) and are asked to make further predictions about future height values or missing values from the table.
The MIDDLE layer would be when they consider: graphing to see that it's a wave, finding wave equation using sinusoidal regression or manual modeling, remembering the connections to unit circle and diameter/amplitude, remembering that they can choose between sine or cosine wave, using the complete wave equation to do further analysis. The middle layer is the trickiest, because it requires that they both have the basic skills (bottom layer) and can extract pertinent info from current problem (top layer), and to put them together in a way to make meaning.
Thanks. I get it now, I think. I guess it doesn't feel like a pyramid to me. Top and bottom are both pretty specific, and middle is problem-solving. (Is it related to Avery's habits of mind?)
ReplyDeleteI think I see what you are getting at...what students need in order are:
ReplyDelete#1) Tools in the toolbox.
#2) An ability to figure out which tools to use when.
#3) An ability to find the raw materials (info) that go with those tools.
I hope the tool metaphor works...is this what you are getting at?
I've created a non-linear version of a problem solving process diagram (see http://davidwees.com/content/problem-problem-solving-process). This is more focused on the process of problem solving itself, whereas your diagram is more focused on the prerequisites students will need to be able to solve problems.
ReplyDeleteMy suspicion is that if you dig deeper, and ask yourself, how will kids pick up these prerequisite skills, it will probably be through mentor-ship, and being given actual problems to solve. Seymour Papert suggests that we start with the problem first, as it motivates the learning of the content and skills required to solve the problem.
I wonder if there is a way to combine our two frameworks together somehow?