Numerous Connections to Quadratic Functions

I think that as secondary math teachers, we ought to be aware of as many ways as possible to model quadratic patterns, so we can seamlessly integrate those techniques into our curricula. It's the first non-straight forward pattern that our kids encounter, and it seems to trouble them throughout their secondary careers. Thankfully, there are ties to quadratic modeling from MANY different topics!

To discuss this concretely, let's first have a look at a quadratic pattern:
(2, 7), (3, 9), (4, 12), (5, 16)

In this discussion, I am going to assume that you've already taught kids how to recognize that this is a quadratic pattern, since that discussion should absolutely precede any quadratic skills, methinks!

Method #1: Helping kids understand at a middle-school level that we find missing coefficients inside equations by plugging in given x's and y's.

For example, given our points above, y = ax^2 + bx + c becomes:
7 = 4a + 2b + c
9 = 9a + 3b + c
12 = 16a + 4b + c

This we can solve in MIDDLE SCHOOL using systems of equations/elimination method.

Method #2: When kids get into high school and they start learning about matrices, we can set the same system up as a problem of 3-by-3 matrix, and help them use the calculator to solve it:


(It's a good time to make sure everyone understands why we're using inverse matrices, and what identity means in math, etc.)

Method #3: Of course, now that they're in the realm of graphing calculators, we should also teach them how to use quadratic regression to get the values of the coefficients.

Method #4: There is another sneakier way of finding the equation using pure quadratics algebra. It's called the Legrange Method, and I learned it this summer at PCMI.

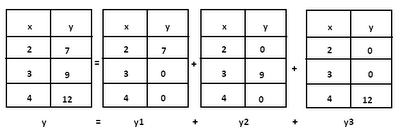
You split the function into smaller, easier quadratic functions by splitting the table and hiding two points at a time:


With a bit of simple algebra, you can figure out that
y1 = 3.5(x - 3)(x - 4)
y2 = -9(x - 2)(x - 4)
y3 = 6(x - 2)(x - 3)

Then, when you simplify each and combine them, you'd get your equation for y! This way is not the easiest, but it does reinforce the idea of roots, plugging in numbers to solve for parts of equation, and expansion/simplification of binomials.

Method #5: Individual elements within a quadratic sequence are created as a summation of arithmetic/linear steps! For example, if you look at the example we have here: (2, 7), (3, 9), (4, 12), (5, 16)

f(2) = 7
f(3) = 7 + 2
f(4) = 7 + 2 + 3
f(5) = 7 + 2 + 3 + 4

Inductively,
f(x) = 7 + { 2 + 3 + 4 + ... +(x-1) }

Or, if we use an arithmetic series formula to represent the sum-of-steps:
f(x) = 7 + [2 + (x-1)][(x-2)/2]

Since my arithmetic series has first term = 2, last term = (x-1), and altogether (x-2)/2 pairs of elements.

Method #6: There is a name for this trick, but I forget what it is. If we draw out the quadratic sequence as dots, we get:

Here I used the gray dots to represent the initial value.

If you double the added dots at each stage (see blue/black dots below), it now becomes instantly easier to find the pattern, because the length and the width of the resulting rectangle is a simple linear progression in terms of x:



f(x) = initial value + half of rectangular area
f(x) = 7 + 0.5(length times width of rectangle)
f(x) = 7 + 0.5(x + 1)(x - 2)

Neat, eh? I think it's pretty amazing how you can approach a simple quadratic pattern from so many different algebraic methods, and I am a true believer that the more of these integrated approaches we take, the better kids will understand each individual method and be able to transfer their knowledge.

By the way, an 8th-grader came up to me and made an insightful observation, the day following our quick class discussion about why we need 3 points in order to find a path of trajectory (quadratic function) using Dan Meyer's basketball pictures. She asked me, "We need 3 points to find a quadratic function, but we need at least 4 points to verify that the pattern IS quadratic, right?" and she drew me a table on the board with some first and second differences. Brilliant! Yes - 3 points is enough to find an equation, but that's like saying two points form a line. That's the minimal amount of info needed to get the equation, but as soon as you have redundant data points, you will know if your regression form is actually correct! How astute of her to make that observation!