We had already discussed right triangle similarity a little bit in our Measurement Unit, when I had taken the kids outside to measure heights of objects using reflections in a pocket mirror. I re-introduced the topic of general similarity this week by asking kids to build congruent and similar parallelograms on the Geoboard. I was more than pleasantly surprised by how DIFFICULT the task was for most of them (honors kids included)!! When I went around and facilitated, I had to guide their attention to slopes of lines, just to get the angles correct in their similar parallelograms. And then, once they had finished constructing (with rubber bands) parallelograms of congruent angles, we discussed as a class why these two are NOT similar:
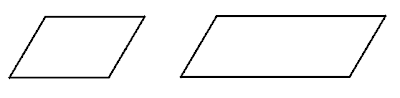
In one class, I was feeling pretty cheeky and I drew this on the board and said, "If you think those are similar, that's like you saying that your face would look the same either here or here."

I think that illustrates non-similarity pretty well (and has a bonus giggle-factor). Afterwards, we used the rubberband parallelograms to practice finding perimeter (Pythagorean Theorem, anyone?) and area (visualization of parallelogram --> rectangle), before launching into a textbook exercise of setting up ratios between similar right triangles to solve for missing sides. Good algebraic practice (involving simplification of square roots, no less), but obviously, this is not what I have in mind for making kids feel EXCITED about trig!
So, I spent part of the afternoon researching options on building inclinometers. The plan is that we'll do one day of flat textbook practice to introduce the basics of trig, then one day "out in the field" measuring tall objects using inclinometers and trig, and then one to two days figuring out where the heck the sine/cosine/tangent values come from, using traditional protractor and ruler. See below. (I can't take credit for this; I'm almost certain I have seen this table format from another teacher at my old school.)



THEN, we'll revisit the Erastothenes video as motivation for inverse trig. (How did Erastothenes find out the angle of the sun relative to the vertical column??)
And, at the end, my kid will (finally, FINALLY) be ready for the Pringles rocket launching goodness. The following blue print is given to me by my awesome physics teacher friend Brian. I haven't built/tested it out yet, but I plan on shooting these more or less straight up to see how high they can go. (Horizontally, I've seen them cover a huge distance, and Brian says that some cannons can send a ball flying for 70 or 80 meters!!)

(And then for my honors kiddies, obviously we'll go into some more advanced stuff, like laws of sine/cosine stuff. I haven't really thought THAT far ahead yet. We'll have to cross the bridge when we get there.)
Thoughts? Suggestions?? Shoot them my way, puh-lease!
It's sad to admit...but your posts have become waaaaay too advanced for me. :( Ha!
ReplyDeleteBTW, congrats!
Thanks, Joyce!
ReplyDeleteTrust me, the topics are not that advanced. I just speak in cryptic Mathteacherspeak, so that I can embed secret messages to other math teachers.
Mimi,
ReplyDeleteYou mentioned similarity and I am teaching that for the first time this year in geometry. I feel like I did a good job of teaching congruence and triangle proofs, so I'm hoping that it will go smoothly. I am amazed at your ability to create scaffolded worksheets and entire units so beautifully. I surprised myself by creating thisfor the beginning of my similarity unit. Could you check it out and give me some feedback? What do you do for similarity?
@Misscalcul8 Nice job on the worksheets! They're beautiful! I liked specifically how #5, #6 makes kids draw similar triangles from scratch, and how #12, #19, #20 are different types of application.
ReplyDeleteI have only two very small suggestions (thanks for thinking I might be helpful!):
1. You may want to start with a hands-on exploration of some sort (Geoboard worked nicely for me, but you can also give kids straws and strings) to make them build similar triangles and then to measure the resulting angles with a protractor. I think that'd emphasize how angles emerge as a result of the ratio'ed side lengths, AND that if you only scaled two sides and not the third side, your triangle would not be similar. (They could see it once they string the triangles together.)
2. The problems you have in the worksheet are quite simple. You can kick it up a notch near the end by having multiple-step similarity, like where they have to find the sides of the second triangle in order to find the sides of the third. ie. 2, 3, 4 to x, y, 10 to y, m, n or something. Not sure. My textbook has some right-triangle problems that are definitely more complicated than this (but those are really complicated for my kids). When I get a chance I'll upload one, if you still have trouble figuring out something.
Also, I liked how you used rectangles. The reason why I use parallelograms is to show that for all shapes, you can't automatically assume similarity when angles are congruent. Only for triangles can you make that assumption!!
Mimi,
ReplyDeleteI already introduced the idea of similarity with
this IMP activity where students constructed different versions of a house and had to figure out which way was appropriate. We've kind of already established the theory of same angles, proportional side lengths, and they're pretty familiar with AA from proving triangle congruence.
I feel like the problems are medium but I also feel like I'm okay with that. I want them to do this on their own with little help from me and I think it will be a confidence boost for them to accomplish that. The next day in class, I plan to throw some harder problems at them on the bell ringer.
From what I can tell, your students seem WAY advanced compared to mind, What do you go by as far as what concepts/skills to teach and how in depth to teach them?
A lot of my honors kids are sharp, but some are just hardworking and they struggle a bit to keep up with the pace/"honors" expectations. About a handful of my regular kids are sharp and hardworking. Another maybe half is regular-regular. They work OK (B- or C-effort) and they need regular assistance from me. The bottom maybe third of my regular classes are really low (in terms of their ability to grasp abstract concepts), so I, their friends, and sometimes their tutors have to really give them a lot of assistance in order to keep them afloat. (In fact, for a while I had a kid whom I would stand next to, 15 minutes at a time, because THAT was how much help he needed and he processed extremely slowly. Eventually they transfered him to a one-on-one situation.) I'd say that in general I have very heterogeneous groups in my regular classes, so multiple-sensory and multiple-mode learning is key for me, since I don't want to lower my expectations.
ReplyDeleteAs far as what to teach... For my 9th-graders, my lessons are activities-driven. I collect a bunch of activities that I think are interesting and that related to a topic, and I go from there to see what concepts I can extract out of them / push my kids to learn. Even the best-behaving 9th-graders can only do so much paper practice in a row before they tune out, so any abstract concepts we do have to be separated by concrete (ie. hands-on) activities that help to build up to more complex ideas.
Does that help? Obviously, I work in a private school... That changes everything.
I guess what I'm asking is, is there a list of standards that you have to teach? What exams are you preparing your students for? Do your students take an exit exam? Or do you choose activities first and then pull concepts out of those?
ReplyDeleteI currently have zero test-prep pressure. Kids don't take any sort of official content exams of any kind here, since it's an international school. I do loosely follow the Geometry textbook in terms of content strands, but my lessons and content are both primarily activities-driven.
ReplyDeleteLike I said, working at a private international school changes... well, everything. I don't have pressure to rush kids along some imaginary race to the finish line.
That does change everything!
ReplyDeleteFor algebra, I'd like to create an investigation on perpendicular and parallel lines. We've just finished slope-intercept and point-slope form. I want them to discover how the slope affects the graph. It would also be nice to tie in x- and y-intercepts and also smoothly transition into systems of equations. Any ideas or suggestions?
You can start with this: http://www.ocf.berkeley.edu/~mimiyang/misc/slopes_of_lines_activity.doc and then add some questions to specifically address your additional objectives of y-intercept and systems of equations. (Maybe have kids record the y-intercepts and observe what happens as they drag the line up/down, OR have them enter additional equations with different y-intercepts in order to compare the graphs.)
ReplyDeleteSince you're interested in having them explore the idea of a system of equations, you can also have them type in specific equations into GeoGebra (via the input bar at the bottom), and then using the "find intersection point" tool to find the point of intersection of multiple lines. Have them plug the points back into both equations to see what would happen. Following that, you should be able to just give them another set of lines and immediately ask them to find the point that satisfies both eqns, etc., and then say at the end of the problem, "This special point is called a SOLUTION to both equations."
Does that help? I don't know off the top of my head how you'd incorporate point-slope and x-intercept into this though. Maybe you can have some guiding question like, "Given any form of the line equation, we can always predict the y-intercept algebraically by plugging x=0 (WHY??), so try to figure a way to predict the x-intercept algebraically. Test out your conjecture by looking on the graph to verify your predicted x-intercept."
Mimi,
ReplyDeleteI like what you created and I want something similar but I want them to graph themselves. I thought this would be a good way to review graphing slope-intercept and point-slope form as well as practice solving equations for y. I don't know how to include x-intercepts either so maybe I will incorporate that into a bell ringer problem or something.
Thanks for your ideas and your help!
Mimi,
ReplyDeleteHere is what I've created so far. Suggestions?
Looks good! But, you should definitely give them an example of when there are two perpendicular slopes that are not 1 & -1. Otherwise many of your kids will walk away remembering that perpendicular slopes are just when you change the sign. (Even if you discuss it with them, it won't "stick" unless they've done it.)
ReplyDeleteThe fractions didn't show up in gdocs but I didn't use 1 or -1 at all. I used 3/4, -4/3, 2/3, and -3/2.
ReplyDelete