They loved it! So far, they can use their calculator to: graph a function (or multiple), find intersection of graphs, find min/max, interpret the min/max given a simple situation, and adjust window ranges. Not a bad basis to have before going into Alg2 next year. We've also reviewed fractional math and reviewed solving systems of equations in context of finding non-integer circumcenters, so I feel like I'm doing an OK job preparing them for the algebra that is to come. For these kids, I also hope to get to maximizing volume problems before the end of the year, in between teaching them proofs and doing 3-D stuff, which I'll be doing with all of my regular students as well.
Anyway, on Friday I introduced the idea of instantaneous and average rates to my Precalc kids using the same video*. The Do Now was a simple review of speed and acceleration terms and making tables of values based on a simple description. (As usual, I was surprised that some of them couldn't do a problem like, "What is the average acceleration per second for a car that starts off at rest and reaches 60mph in 3 seconds?") Then, I reviewed with them how to set up the quadratic equation for projectiles before watching the Pringles cannon video*. They noted that the ball was in the air between t=4 and t=9, so I had them graph the function H(t) = -4.9(t-4)(t-9) in their calculator, and they then used the tables in the graphing calculator to fill out this table below. For t values, they used t=4, t=4.5, t=5, etc. ...going up in half-second increments, all the way through t=9. I had to guide them through how to do the averages, while they worked in pairs.

Once they filled out the tables, natural questions arose as they compared their results for the last two columns. I went around to probe why each pair of kids thought that the half-second "speed" (I guess I should have said velocity, to be more precise) is decreasing and becomes negative in the right-most column. They were excited to be able to figure out why all on their own! It's physics in action!! And then, as a class we discussed why the "average speed since launch" actually becomes zero the moment that you land on the ground. One kid raised his hand and explained to the class that it's because your overall change is zero at that point, so therefore your average speed is zero. --Awesome!! In our discussions, I used the term "instantaneous" loosely to describe what's been happening in the last 0.5 seconds (4th column), to distinguish it from what's been happening since the beginning (3rd column).
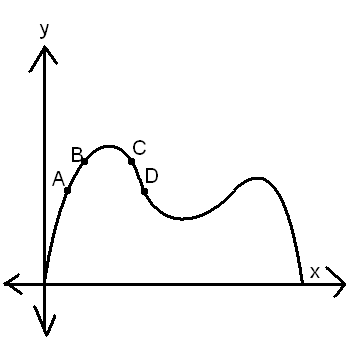
It was awesome. Later on I drew a graph on the board like this and asked them to describe the "speeds" between different points AB, CD, and AD. The class comfortably told me that AB has positive speed, CD has negative speed, and AD has zero speed. Good conceptual basis for next week, when we move into the actual algebra of finding instantaneous and average rates! I hope that this activity will "stick" with them, so that when they look at graphs in the future to analyze rates, it won't just seem like some abstract concept.
* Most of them had built and shot their own Pringles cannons in physics this year, so I felt like it was OK to just use the video instead of wasting time going outside to do the same thing again.
PS. I suppose I should mention that Obama is coming to El Salvador. School's not in session on Tuesday and Wednesday for street closure reasons. Selfishly, I feel a bit of relief that this comes 2 days before quarter 3 grades are due, even though it means that there is some instruction time lost, obviously.
No comments:
Post a Comment