We are in the thick of it now, the part of the semester when I see how kids handle setbacks and challenges. This is one of the ways I really get to know a kid, because I truly believe that how you handle setbacks defines your character. I tell the kids that they can keep reviewing and re-quizzing, or re-submitting drafts of a writing assignment, until they decide that their score is good enough to stop. No one is going to disallow them to keep working to get better, because I think that training kids to keep tackling something long after the class has "moved on" is how we can teach them to develop a persevering character.
For me personally, I've always viewed myself as a second-try kind of gal. If I weren't, I would have given up the first time a teaching program told me that I wasn't their ideal candidate, and I would never have ended up doing what I do, and loving it. Too many adults give up on their goals too easily, and let other people decide for them what they can and cannot achieve. I don't want that to happen to my students.
Anyhow, enough philosophizing. More about teaching. My Calculus kids are entering a very interesting phase of the course. We had our first quiz, which was quite tricky and conceptual, even though it did not involve many numbers. To my delight, about two-thirds of the class did quite well on this quiz, and the top three or so scores were all girls!!! I cannot help myself but feel gleeful about that, especially because 1. the girl who did the best on the quiz (missed actually none of the problems, including the bonus ones which we had only briefly seen during class) had previously said to me that she always felt a little behind in other people's math classes, and 2. our school has been having some conversations surrounding issues of diversity (mainly ethnic and socioeconomic), which has been making me wonder a bit about the role of "male privilege" in the math classroom, similar to the issues of "white privilege." Anyhow, the fraction of kids who didn't do so well on their quizzes are seeing me on Tuesday for a re-quiz, so as of now it is still too early for me to say whether they just had a bad day, or they are still learning how to study effectively, or they really need some serious intervention with the topics that we have covered. In this class, unlike the other classes, I have not been collecting/grading homework past discussing the answers as a group, since thus far we have been building up introductory concepts and there are not a lot of nitty-gritty skills checkpoints for me to look at and respond to. I think that contributed to the lack of individual feedback before the first quiz, which I will remedy in the coming unit by being more hands-on with grading their homework assignments, once we step into the realm of manual differentiation techniques. Overall, I have been very happy with the way that my kids have built their conceptual understanding around derivatives and instantaneous and average rates. We take every second Friday to review algebra skills from the past, and then I assign a review homework assignment for the weekend following. So far, we have reviewed: 1. factorization techniques, 2. how to solve for a parameter within an equation, and 3. when to use their calculators to solve complex equations; and already I can see their independence growing inside the classroom from these mini skills reviews. We just wrapped up a great worksheet (if I may say so myself), because every problem in this worksheet is anchored in something very real. Problem 1 was about investment, and I had talked to the kids about how my husband does real-estate investment and how he uses this type of math to calculate mortgage rates and monthly expenses on a rental property, in order to compare those fees with his rental income to make sure that he will clear a profit every month from his investment. (Related to this I talked to the kids about why they should invest, and why investment does not mean that they cannot be contributing productively to the society.) Problem 2 was about carbon-dating, but the kids needed to read the initial C14 levels out of a graph of atmospheric carbon levels to use in their carbon decay model. This is very realistic, and we got to talk a little bit about the science behind your body equalizing with the atmospheric carbon levels while you are breathing/alive, as well as about how cow-farming is causing historic carbon levels to rise (connecting this to what they see in the graph of historical atmospheric levels). Problem 3 on the worksheet is an ad that I actually found on the web for Gap Inc's credit card offers, so although it is another review problem for interest rates, it is steeped in real world context. I am trying to make my Calculus class as inter-curicular as possible on a day-to-day basis, so that kids can see the reason/motivation behind studying what we study. Interestingly enough, a couple of the faster-moving kids have already started on our end-of-unit economic mini-project (Part 1 and Part 2), and the first question they asked me before even starting the math was, "Why would anybody care about marginal costs?" --Aren't my kids fabulous? I want them to ask me questions like this, so that Calculus can come alive for them.
Anyhow, Precalc is also going swimmingly. I heard feedback from one 11th-grade advisor that her advisee loves my class, and thinks that all the math we do thus far is very clear and very understandable. The students are in the process of finishing up their first big lab writeup, which was very exciting because when I took them down to the computer lab, I got to show them how to 1. enter and format equations properly into MS Word or Google Docs, and 2. how to connect their TI-84s to the computer via TI-ScreenConnect to prove that they are doing the tests of their formulas. Some of the kids, in fact, didn't even know how to construct tables or write subscripts, so there was lots of tech education there, besides helping them out with the mathematical language. The kids thought that typing up their revisions to the rough drafts was going to be easy, but it did in fact take them two full (45-minute) class periods, and many still had to go home to take some time this weekend to re-read through it to make sure that they have hit every part of the project rubric. Anyhow, I prepared a graphical organizer template so that sometime next week, we can discuss how this idea of approaching and analyzing math sequences is going to be the big idea through the entire first Quint. (We have 5 Quints a year, as opposed to 4 Quarters.) Also, something quite cool that I tried recently was to put kids into groups and let them do mixed analysis of linear and quadratic sequences, and instead of me telling them whether they were correct, they got to check using the web interface of visualpatterns.org! The kids were super into it, and I think seeing the two types side by side really helped them to clarify mentally the different strategies for each type. Alongside the writeups, the kids have just about finished reviewing all the algebra skills for lines, so I will give another quiz next week before moving on to reviewing quadratic and transformational skills.
My Algebra 2 classes are moving pretty slowly through their regression project, because I have discovered that they have some holes in their Algebra 1 knowledge and am taking some daily class time to discuss homework problems before assigning new review assignments. In class, we are doing white-boarding practice about once a week, because it is a great time for me to make sure that everyone is doing some algebra practice together and getting instantaneous feedback/help as needed. Following our fairly difficult first quiz, which I had written about last week, lots of kids came to see me to do re-quizzes, which I loved. Although they didn't all get 100% on their re-quizzes, it started a very productive dialogue with kids about how they are studying, what study tips I can recommend, and why things always seem easier when you do a re-quiz. One international student in particular had an 180-degree shift of attitude towards me after the re-quiz. I think she's the kind of student who thrives particularly on positive feedback, so the fact that she had failed the first time but got 100% on the second try, really boosted her confidence and her feelings towards math (and I guess, me). So, although it had been a challenging/"discouraging" week last week, I think it was a necessary reality check for many kids and now they are much more focused and strategic in their learning. My 10th-graders, for example, took a lot of photos yesterday during our white-boarding practice, because the one student who had done that last time and who had practiced with those problems later at home, had done very well on the quiz and had offered that up as a study strategy to her peers. So, we are a growing community of learners, moving in the right direction, slowly but surely!
For both Algebra 2 classes, on Monday we will go and test out the kids' predictions for the bungee drop. They will build the cords, name their rubber chickens, take a photo with their chickens, and then we will go out to the balcony. It'll be a very fun day, but the hard work that is yet to come is to write the lab reports coherently. I am a little nervous about getting their rough drafts on Tuesday, and what those will look like, especially for my international kids....
But, I cannot complain. I love this time of the year!
Showing posts with label grade9. Show all posts
Showing posts with label grade9. Show all posts
Saturday, September 28, 2013
Saturday, September 21, 2013
Week 2 Teaching - the Gentle Push Back
The second full week of school has been a very meaty one. The kids seemed very eager to learn after the first few unstructured socializing/cohort retreat days. And I am starting to see the various personalities starting to emerge, which is both wonderful and more challenging because now it is real teaching and real learning.
In my Algebra 2 classes, we had our first quiz, which challenged all the students in different ways. My vision for the start of Algebra 2 had been to lay down a solid tech foundation alongside review or re-teaching of linearity skills, so that kids realize that a corner stone of Algebra 2 has to be using technology flexibly in order to self-monitor accuracy. I told the kids that I don't want them to ask me, "Is this right?" but I would be very happy to hear them ask, "How can I check this using the calculator?" So, on the first quiz they needed to demonstrate this skill throughout the algebra problems, in order to earn full points on reflection. (I gave separate points for: Communication, Approach, Accuracy, and Reflection.) In the end, my two groups were challenged differently; the Grade 10 native-speaker class had holes in their algebra skills and couldn't complete all problems, and the Grade 9 largely non-native speaker class generally showed stronger algebra skills (even with less in-class whiteboarding practice), but struggled with using the calculator flexibly. But, some of the kids shared their effective studying strategies in class, and some of the other kids are planning to see me on Monday for a requiz, so I feel quite hopeful that this first quiz is just the start of a learning dialogue.
By the way, my relationship with the international kids is developing in an interesting way. Because I speak Chinese, I am able to help the kids in my class without watering down the level of tasks I am asking them to complete. But, at the same time I can carry some weight when I see them being off-task and I offer to call their parents in China to have the dialogue directly about their efforts, in Chinese. What an interesting situation for me and them. Interestingly, they are better-behaved for me, and they try hard to speak English in my class, except when they need to help each other translate something. I am curious how they are going to do on their first big writing assignment, which we will be doing next week...
In my Precalculus class, kids are wrapping up the rough drafts of their first big project on special (triangular and stellar) numbers. I had to be very explicit in helping them to format their writeup. (I had to say at one point, "Take out a sheet of paper. At the top, write, 'In this task, I was asked to...' Now, complete that thought in your own words. I give you 30 seconds to do that. ...Now, write down, 'In order to accomplish that, first we had to...' and go ahead and complete that thought, make sure you insert a diagram here." But, after about 5 minutes of modeling, I think they all got the idea and were able to continue the rest at home, because all the drafts that they brought back to me the next day looked pretty coherent. So, it has been a tough project for them, for sure, but I still think it had tremendous learning value. We also had a quiz, and the kids are doing fine with function identification, interpretation of f(3)=7, and writing both recursive and explicit equations for arithmetic sequences. Some of the more clever ones were able to write formulas for quadratic sequences already, based on their learning from the Special Numbers project. So, I am pretty happy so far. As we wrap up our project (meaning, as I read over their drafts), the kids are doing mixed lines review and checking all answers via their calculator. They use either the Table or Trace to check all equations that they write from given info, and they use [2nd][Math] to verify equivalent expressions after simplifying. So far, so good, because kids in this class seem to be quite independent.
In my Calculus class, I had one student come forward to say that he really enjoys the exploratory nature of our class, and two others who came to ask me to do more examples followed by practice. I thought over this carefully and decided that although I think it is awesome that kids are being advocates for their own learning, and I really wanted to acknowledge that and to encourage that, the issue is really much more complex than their individual learning styles. I ended up describing to the class two contrasting learning models, direct instruction and inquiry-based learning. I said that in most math classes they have had, they probably experienced the former (intro, example, guided example, individual practice, closure, and eval), and that that is fine. It is comfortable, you know what to expect when you come to class. But, that way only reaches the top half of the class, the half that is fortunate enough to maintain focused attention and to comprehend at the speed of material presentation. Then I showed them a diagram of inquiry-based learning, which is a cycle of asking questions, investigation, creation of model or new knowledge, discussion, reflection, and back to asking questions. I explained to them that what we do in class is NOT true inquiry, because true inquiry would be like me saying, "Go. Find out how much universal health care is going to cost our country, both in the short run and in the long run." The problem would be entirely open-ended, complex, and vast, and we would learn all the necessary math skills as we move along. I explained to them that what we do typically in our class is a smaller version of this; within the individual topics of Calculus, I try to think about ways to structure our class so that they can create their own understanding. I ended the class with showing a little clip from Sir Ken Robinson's tedX talk (the animated one), and saying that teaching creativity is hard, and that our traditional schools have been doing a good job killing creativity. I told the kids that, yes, I think even in math there is room for creativity in the classroom, and unfortunately we don't get that by me doing an example and then handing out 25 problems that look the same. So, although I will try to find a balance between direct instruction and exploratory learning, I want the kids to keep an open mind and to appreciate opportunities for creativity in any discipline.
After this talk, I heard from another student in this class who said that she really enjoys math this year, and that our chat helps her to understand and appreciate my philosophy even more. So, one point for being authentic with kids and treating them as intellectual equals.
Good second week. Our school is awesome, by the way. I love that kids clean the school three times a week, and I adore my colleagues!!!!!
In my Algebra 2 classes, we had our first quiz, which challenged all the students in different ways. My vision for the start of Algebra 2 had been to lay down a solid tech foundation alongside review or re-teaching of linearity skills, so that kids realize that a corner stone of Algebra 2 has to be using technology flexibly in order to self-monitor accuracy. I told the kids that I don't want them to ask me, "Is this right?" but I would be very happy to hear them ask, "How can I check this using the calculator?" So, on the first quiz they needed to demonstrate this skill throughout the algebra problems, in order to earn full points on reflection. (I gave separate points for: Communication, Approach, Accuracy, and Reflection.) In the end, my two groups were challenged differently; the Grade 10 native-speaker class had holes in their algebra skills and couldn't complete all problems, and the Grade 9 largely non-native speaker class generally showed stronger algebra skills (even with less in-class whiteboarding practice), but struggled with using the calculator flexibly. But, some of the kids shared their effective studying strategies in class, and some of the other kids are planning to see me on Monday for a requiz, so I feel quite hopeful that this first quiz is just the start of a learning dialogue.
By the way, my relationship with the international kids is developing in an interesting way. Because I speak Chinese, I am able to help the kids in my class without watering down the level of tasks I am asking them to complete. But, at the same time I can carry some weight when I see them being off-task and I offer to call their parents in China to have the dialogue directly about their efforts, in Chinese. What an interesting situation for me and them. Interestingly, they are better-behaved for me, and they try hard to speak English in my class, except when they need to help each other translate something. I am curious how they are going to do on their first big writing assignment, which we will be doing next week...
In my Precalculus class, kids are wrapping up the rough drafts of their first big project on special (triangular and stellar) numbers. I had to be very explicit in helping them to format their writeup. (I had to say at one point, "Take out a sheet of paper. At the top, write, 'In this task, I was asked to...' Now, complete that thought in your own words. I give you 30 seconds to do that. ...Now, write down, 'In order to accomplish that, first we had to...' and go ahead and complete that thought, make sure you insert a diagram here." But, after about 5 minutes of modeling, I think they all got the idea and were able to continue the rest at home, because all the drafts that they brought back to me the next day looked pretty coherent. So, it has been a tough project for them, for sure, but I still think it had tremendous learning value. We also had a quiz, and the kids are doing fine with function identification, interpretation of f(3)=7, and writing both recursive and explicit equations for arithmetic sequences. Some of the more clever ones were able to write formulas for quadratic sequences already, based on their learning from the Special Numbers project. So, I am pretty happy so far. As we wrap up our project (meaning, as I read over their drafts), the kids are doing mixed lines review and checking all answers via their calculator. They use either the Table or Trace to check all equations that they write from given info, and they use [2nd][Math] to verify equivalent expressions after simplifying. So far, so good, because kids in this class seem to be quite independent.
In my Calculus class, I had one student come forward to say that he really enjoys the exploratory nature of our class, and two others who came to ask me to do more examples followed by practice. I thought over this carefully and decided that although I think it is awesome that kids are being advocates for their own learning, and I really wanted to acknowledge that and to encourage that, the issue is really much more complex than their individual learning styles. I ended up describing to the class two contrasting learning models, direct instruction and inquiry-based learning. I said that in most math classes they have had, they probably experienced the former (intro, example, guided example, individual practice, closure, and eval), and that that is fine. It is comfortable, you know what to expect when you come to class. But, that way only reaches the top half of the class, the half that is fortunate enough to maintain focused attention and to comprehend at the speed of material presentation. Then I showed them a diagram of inquiry-based learning, which is a cycle of asking questions, investigation, creation of model or new knowledge, discussion, reflection, and back to asking questions. I explained to them that what we do in class is NOT true inquiry, because true inquiry would be like me saying, "Go. Find out how much universal health care is going to cost our country, both in the short run and in the long run." The problem would be entirely open-ended, complex, and vast, and we would learn all the necessary math skills as we move along. I explained to them that what we do typically in our class is a smaller version of this; within the individual topics of Calculus, I try to think about ways to structure our class so that they can create their own understanding. I ended the class with showing a little clip from Sir Ken Robinson's tedX talk (the animated one), and saying that teaching creativity is hard, and that our traditional schools have been doing a good job killing creativity. I told the kids that, yes, I think even in math there is room for creativity in the classroom, and unfortunately we don't get that by me doing an example and then handing out 25 problems that look the same. So, although I will try to find a balance between direct instruction and exploratory learning, I want the kids to keep an open mind and to appreciate opportunities for creativity in any discipline.
After this talk, I heard from another student in this class who said that she really enjoys math this year, and that our chat helps her to understand and appreciate my philosophy even more. So, one point for being authentic with kids and treating them as intellectual equals.
Good second week. Our school is awesome, by the way. I love that kids clean the school three times a week, and I adore my colleagues!!!!!
Labels:
algebra2,
calculus,
grade11,
grade9,
math stuff,
precalculus
Wednesday, September 11, 2013
Week 1 Teaching
My year at school has begun, and as of today, we have had a full 5 days' worth of classes, even though lots of kids were missing class here and there for special retreat-type of activities. I feel quite settled, and I am starting to learn most of the kids' names despite having a terrible memory.

I am thrilled about how Precalculus is going! It's almost too good to be true -- the kids can build their own patterns from colored blocks; they can write recursive equations to represent those patterns; they can explain the limitations of knowing only the recursive formulas; they can write explicit equations that turn out to be linear; they can sum arithmetic elements and explain why that sum must be quadratic, both from a graphical standpoint and an algebraic standpoint. And they're ready to break down quadratic patterns into linear elements, in order to find the formula for the n-th quadratic element! ...Rock ON, 11th-graders!! They will start their first project very soon, either tomorrow (if they understand all preceding concepts) or next week. It is a project that I adopted from the IB, watered down quite a bit simply because I don't want the kids to be scared off right away.
My vision of tying linearity and quadratics neatly together for the kids with the concept of sequences is working out well so far; we'll see how they fare on the first quiz! :)
In Calculus, I discovered on Day 1 that the kids were strangers to the powers of the graphing calculator. I spent the next day walking them through basic features, and since then they've been flying through the conceptual material which I've presented through explorations. Unfortunately, this class has had the most amount of absences, since the Seniors and various special leadership folks had to miss class starting on Tuesday of this week. That has caused the pacing to be a bit chaotic. The kids who have been here everyday now have a solid grasp of the derivative: what it is, how to read it from the calculator, and how it relates to average rate. They can visualize derivative graphs when looking at an abstract original graph of f, and in general I think their calculator skills are slowly maturing. Yay!
My Algebra 2 classes are two diverse groups. One is full of international students, some of who had just stepped off the plane to arrive in America with very little English comprehension. This has made for a very interesting challenge, trying to teach those kids in the same class as the native speakers. I think it is great -- it helps to teach all kids the virtues of patience and kindness, because some of the non-native speakers are much stronger in math than some of their native-speaking peers, so in my mind at least, it's a bit of give-and-take for everyone. The other Algebra 2 class is full of bubbly tenth-graders, and most of them are my advisees. I simply love that class! They don't work as fast as the other group through the material, but they're very responsible, eager to learn, and nice. Kids from my Grade 10 class keep saying that that seems like the fastest-passing period, and they seem to genuinely enjoy their time in class even though we're still on the nitty gritties of basic algebra. We're working our way through some knowledge about how to use the graphing calculator flexibly to check our work alongside reviewing skills from Algebra 1 and wrapping our mind around visual linear patterns. The first big project will be coming up soon though (next week!), and it's the rubber chicken bungee jumping project (I think at most schools, they use barbies), which will involve a significant amount of writing and really show kids what I expect this year from their analyses. Whee! I'm excited!
How are your school years going??

I am thrilled about how Precalculus is going! It's almost too good to be true -- the kids can build their own patterns from colored blocks; they can write recursive equations to represent those patterns; they can explain the limitations of knowing only the recursive formulas; they can write explicit equations that turn out to be linear; they can sum arithmetic elements and explain why that sum must be quadratic, both from a graphical standpoint and an algebraic standpoint. And they're ready to break down quadratic patterns into linear elements, in order to find the formula for the n-th quadratic element! ...Rock ON, 11th-graders!! They will start their first project very soon, either tomorrow (if they understand all preceding concepts) or next week. It is a project that I adopted from the IB, watered down quite a bit simply because I don't want the kids to be scared off right away.
My vision of tying linearity and quadratics neatly together for the kids with the concept of sequences is working out well so far; we'll see how they fare on the first quiz! :)
In Calculus, I discovered on Day 1 that the kids were strangers to the powers of the graphing calculator. I spent the next day walking them through basic features, and since then they've been flying through the conceptual material which I've presented through explorations. Unfortunately, this class has had the most amount of absences, since the Seniors and various special leadership folks had to miss class starting on Tuesday of this week. That has caused the pacing to be a bit chaotic. The kids who have been here everyday now have a solid grasp of the derivative: what it is, how to read it from the calculator, and how it relates to average rate. They can visualize derivative graphs when looking at an abstract original graph of f, and in general I think their calculator skills are slowly maturing. Yay!
My Algebra 2 classes are two diverse groups. One is full of international students, some of who had just stepped off the plane to arrive in America with very little English comprehension. This has made for a very interesting challenge, trying to teach those kids in the same class as the native speakers. I think it is great -- it helps to teach all kids the virtues of patience and kindness, because some of the non-native speakers are much stronger in math than some of their native-speaking peers, so in my mind at least, it's a bit of give-and-take for everyone. The other Algebra 2 class is full of bubbly tenth-graders, and most of them are my advisees. I simply love that class! They don't work as fast as the other group through the material, but they're very responsible, eager to learn, and nice. Kids from my Grade 10 class keep saying that that seems like the fastest-passing period, and they seem to genuinely enjoy their time in class even though we're still on the nitty gritties of basic algebra. We're working our way through some knowledge about how to use the graphing calculator flexibly to check our work alongside reviewing skills from Algebra 1 and wrapping our mind around visual linear patterns. The first big project will be coming up soon though (next week!), and it's the rubber chicken bungee jumping project (I think at most schools, they use barbies), which will involve a significant amount of writing and really show kids what I expect this year from their analyses. Whee! I'm excited!
How are your school years going??
Friday, June 7, 2013
3-D Surface Area and Volume Projects: 2013 Edition
Here are the 3-D project photos from this year. I kept only the yellow tower and the red-and-yellow rocket from last year, so everything else on the shelves is new! As usual, they had to calculate volume, surface area, and draw 3-D designs and 2-D nets. Even though concavities were optional, many groups decided to build in concavities into their designs / calculations this year.
Afterwards, our tests were not easy, but the kids did quite well! In fact, the student who did the "star" project shown in the first picture (5 pyramids connected to a pentagonal prism, with a rectangular prism concavity) got 100% on her test, which made both her and me totally excited!!!!
Among other test problems, I offer you these two to try with your students. These problems integrate the flexible application of formulas with the necessary skill of visualization of volume and surface area. For an easy differentiation, you can replace one of the sides with x, and ask them to find an abstract formula for the SA or volume.
Calculate volume and surface area:
Calculate just surface area.
(Only standard circle equations for area and circumference are given.)
Wednesday, May 22, 2013
If only all right triangles were this cute...
Hi, I'm teaching trig to my ("low" math group) 9th-graders, and loving it. We only had time for 1 day of trig lesson before we will have to concentrate on reviewing for the end-of-year test (after which we'll come back and do some outdoors trig/angles of elevation and depression type of stuff, leading into complicated trig word problems). The kids were awesome at basic trig! They learned how to apply sine, cosine, and tangent correctly and consistently in one 80-minute period. Rock stars, these kids. They use the tactile trick to figure out which side is opposite, adjacent, and hypotenuse, and then they use cross-multiplication to consistently and correctly solve for x. For now, since we're only learning the whole of right-triangle trig in one day, I am going to give them the acronym SOH-CAH-TOA on the exam and just require them to remember what the acronym stands for. Eventually, they'll have to memorize SOH-CAH-TOA, obviously.
Anyway, totally apropos, this totally cracked me up today.
Anyhow, this week is a killer. I keep trying to get ahead, but it seems impossible, as I am pulled in all directions as a teacher, a department chair, and a person soon to move across a big pond. I wonder when the next sigh of relief will come. Hopefully, there is one scheduled before July...
Anyway, totally apropos, this totally cracked me up today.
Anyhow, this week is a killer. I keep trying to get ahead, but it seems impossible, as I am pulled in all directions as a teacher, a department chair, and a person soon to move across a big pond. I wonder when the next sigh of relief will come. Hopefully, there is one scheduled before July...
Friday, April 19, 2013
Quadratic Function Project Brainstorm
I'm brainstorming / laying out my end-of-year plans for my 8th-graders. After their end-of-year exam in late May, we will close grades, but we will still have about 3 or so weeks of instruction, which is enough time to do something very rich and not have to coordinate with other classes (since we use the May test to do placement for Grade 9). Last year, I used this extra time to let the 8th-graders define their own math projects, which were plenty of fun, but I wasn't entirely happy with the rigor of their mathematical results. This year, I'm toying with the idea of doing an exploratory quadratic functions unit. (Technically, quadratic FUNCTIONS are a Grade 9 topic for us, but previewing it in Grade 8 is always beneficial.)
I'm thinking of making it largely exploratory, since by then pacing won't be much of an issue and I can let them really take the time to develop their conceptual understanding of quadratic functions, which is the essential access point to a lot of higher-level algebra analysis down the road.... The timing is tight (as it was last year with my other end-of-year projects), but I think it's still doable and has a lot of potential!!!
Let me know what you think. Is it an OK approach for intro to quadratic functions / basic function transformations?? This is based on my rumination about a different way to think about flexible factorization of quadratic functions.
Day 1: Developing the understanding of how to graph y = x2 + bx.
Plan - In pairs, kids will be given y = x2 + 2x, y = x2 + 5x, y = x2- 3x, y = x2 - 7x. to graph on the calculator. They will sketch results in their notes, recording all intercepts in the form (x, y), and writing a one-sentence hypothesis about what the graph of y = x2 + bx will look like.
Then, they will be reminded that in a function, we can solve for the x-intercept(s) by setting the height of the point, y, equal to zero. They will algebraically show that their hypothesis works for all b values.
Day 2: Developing the understanding of how to graph y = ax2 + bx, which is a more general version of the quadratic function.
Plan - In pairs, kids will be given y = x2 + 6x, y = 2x2 + 6x, y = 3x2 + 6x, y = 12x2 + 6x. They will again sketch graphs, noting x-intercepts, and then make a hypothesis about the effect of the leading coefficient on the graph. They will show how to solve for the x-intercepts using algebra only.
Day 3: Developing the understanding of how the graph is affected by the sign of its leading coefficient.
Plan - In pairs, kids will be given y = -x2 + 6x, y = -2x2 + 6x, y = -3x2 - 6x, y = -12x2 - 6x. They will again sketch graphs, noting x-intercepts, and then make a hypothesis about the effect of the leading coefficient on the shape of the graph. They will show how to solve for the x-intercepts using algebra.
As part of Day 3, they will do some matching between equations and pictures of graphs and to justify their choices orally.
By the end of Day 3, they should also be able to explain in writing how to graph y = ax2 + bx.
Day 4: Developing the understanding of the effect of the constant term c.
Plan - In pairs, the kids will put in a function like y = x2, and look at its table in the calculator. They will be asked to generate a second function that would increase all y-values by 1. They will prove their new equation works, by showing the values of both functions side by side in the calculator (y1 and y2), and copying down the table values. Then, they will write down the formula for the new function.
They will then look at the graphs of the two functions to determine "what happened" visually to the original graph when the equation got changed that way.
They will keep playing around with this idea, translating upwards and downwards and checking both the table and the graph to observe/verify the effect of c.
By the end of Day 4, they will be given a graph of two functions. One of the functions will have an accompanying formula, and they will be able to see visually what happened to the points on the graph. They will then need to "guess" at the equation of the other, vertically shifted function, and verify it in the calculator.
Day 5: Putting the algebra pieces altogether
Plan - One partner of the pair will have a set of sequenced instructions, to be given to their partner one step at a time. The first step will sound like, "Sketch a graph of y = x2 - 9x, labeling x-intercepts with values." Then, after that has been successfully completed, the next instruction will be given: "Now sketch the result of shifting that graph vertically up 4 units, labeling the resulting images of those original points you knew." After that has been done, the partner gives the third instruction: "Now, write the formula for this new graph." Once the partner is finished, they verify their results using the graphing calculator's graphing and table features and write a brief explanation of how they checked their results. Then, they switch, and the new partner has instructions that has to do with a downwards facing function like y = -x2 - 6x, and repeat a similar sequence of instructions to generate a new graph, a new / related equation, and to verify all results against the calculator.
Both partners will then work together to complete problems starting with functions of the form
y = ax2 + bx and translating those graphs vertically to get new graphs.
By the end of Day 5, they should be able to explain the connection between y = ax2 + bx and
y = ax2 + bx + c, and explain how to use this connection to graph any standard-form quadratic function quickly in under 1 minute.
Day 6: Practicing/drilling the connection between quadratic function equation and graphs
Plan - In pairs, they will start with a function y = x2 - 9x + 1, highlight the first two terms, sketch that function using dashed lines, and then sketch in the "real" final function using solid line. They will repeat this a few times with different functions, until they can fluidly graph any y = ax2 + bx + c function. On this day, they'll also learn to visualize the axis of symmetry and to write its equation by inspection of graph.
Day 7: Going backwards from a graph to an equation
Plan - In pairs, they will be given one quadratic graph with two "nice", symmetric integer points being emphasized on the graph, one of the points being on the y-axis. They will be asked to sketch using dashed lines what this function would look like if you shifted those two points down to the x-axis, and be asked to write the function equation of both graphs. They will practice this a few times.
At the end of Day 7, they will be given a quadratic graph whose two "nice", symmetric integer points are both not on the y-axis. This tests them to see if they can figure out that the translated graph would have an equation that looks like y = (x - m)(x - n) + p instead of y = x(x - n) + p
Day 8: Playing around with the idea of adjusting "a".
Plan - In pairs, they will import Dan Meyer's basketball photo into GeoGebra. We will discuss as a class the need to find a modeling equation in order to fully predict whether the ball will make it into the hoop. From there, they will choose two nice integer points, write the equation, and graph. If they notice that the curve goes through those two points but doesn't have the correct steepness desired in order to fit the photo, then they will create a slider value in GeoGebra and toggle the value of "a" until they get a good "fit" around the graph, and record their results.
As a class, we will then go over the idea of solving for "a" using an unused point (x, y) and link it to solving for the y-intercept in linear functions. They will solve for "a" this way to compare analytical results against the technology results.
Day 9: Modeling Individually
Plan - Following a discussion of examples of parabolic applications, each pair will find and import their own photos of "real-life" parabolic shapes from the web. They will then model the function in Geogebra both using technology and using algebraic analysis.
Day 10: Creating posters
Plan - Each pair will create two posters, one with the modeled functions overlaying the photos, and one poster explaining the general process of graphing y = ax2 + bx + c and the general process of fitting an equation to a parabolic graph.
Day 11: Practice presentations
Day 12: Math fair for other classes / parents?!
I'm thinking of making it largely exploratory, since by then pacing won't be much of an issue and I can let them really take the time to develop their conceptual understanding of quadratic functions, which is the essential access point to a lot of higher-level algebra analysis down the road.... The timing is tight (as it was last year with my other end-of-year projects), but I think it's still doable and has a lot of potential!!!
Let me know what you think. Is it an OK approach for intro to quadratic functions / basic function transformations?? This is based on my rumination about a different way to think about flexible factorization of quadratic functions.
Day 1: Developing the understanding of how to graph y = x2 + bx.
Plan - In pairs, kids will be given y = x2 + 2x, y = x2 + 5x, y = x2- 3x, y = x2 - 7x. to graph on the calculator. They will sketch results in their notes, recording all intercepts in the form (x, y), and writing a one-sentence hypothesis about what the graph of y = x2 + bx will look like.
Then, they will be reminded that in a function, we can solve for the x-intercept(s) by setting the height of the point, y, equal to zero. They will algebraically show that their hypothesis works for all b values.
Day 2: Developing the understanding of how to graph y = ax2 + bx, which is a more general version of the quadratic function.
Plan - In pairs, kids will be given y = x2 + 6x, y = 2x2 + 6x, y = 3x2 + 6x, y = 12x2 + 6x. They will again sketch graphs, noting x-intercepts, and then make a hypothesis about the effect of the leading coefficient on the graph. They will show how to solve for the x-intercepts using algebra only.
Day 3: Developing the understanding of how the graph is affected by the sign of its leading coefficient.
Plan - In pairs, kids will be given y = -x2 + 6x, y = -2x2 + 6x, y = -3x2 - 6x, y = -12x2 - 6x. They will again sketch graphs, noting x-intercepts, and then make a hypothesis about the effect of the leading coefficient on the shape of the graph. They will show how to solve for the x-intercepts using algebra.
As part of Day 3, they will do some matching between equations and pictures of graphs and to justify their choices orally.
By the end of Day 3, they should also be able to explain in writing how to graph y = ax2 + bx.
Day 4: Developing the understanding of the effect of the constant term c.
Plan - In pairs, the kids will put in a function like y = x2, and look at its table in the calculator. They will be asked to generate a second function that would increase all y-values by 1. They will prove their new equation works, by showing the values of both functions side by side in the calculator (y1 and y2), and copying down the table values. Then, they will write down the formula for the new function.
They will then look at the graphs of the two functions to determine "what happened" visually to the original graph when the equation got changed that way.
They will keep playing around with this idea, translating upwards and downwards and checking both the table and the graph to observe/verify the effect of c.
By the end of Day 4, they will be given a graph of two functions. One of the functions will have an accompanying formula, and they will be able to see visually what happened to the points on the graph. They will then need to "guess" at the equation of the other, vertically shifted function, and verify it in the calculator.
Day 5: Putting the algebra pieces altogether
Plan - One partner of the pair will have a set of sequenced instructions, to be given to their partner one step at a time. The first step will sound like, "Sketch a graph of y = x2 - 9x, labeling x-intercepts with values." Then, after that has been successfully completed, the next instruction will be given: "Now sketch the result of shifting that graph vertically up 4 units, labeling the resulting images of those original points you knew." After that has been done, the partner gives the third instruction: "Now, write the formula for this new graph." Once the partner is finished, they verify their results using the graphing calculator's graphing and table features and write a brief explanation of how they checked their results. Then, they switch, and the new partner has instructions that has to do with a downwards facing function like y = -x2 - 6x, and repeat a similar sequence of instructions to generate a new graph, a new / related equation, and to verify all results against the calculator.
Both partners will then work together to complete problems starting with functions of the form
y = ax2 + bx and translating those graphs vertically to get new graphs.
By the end of Day 5, they should be able to explain the connection between y = ax2 + bx and
y = ax2 + bx + c, and explain how to use this connection to graph any standard-form quadratic function quickly in under 1 minute.
Day 6: Practicing/drilling the connection between quadratic function equation and graphs
Plan - In pairs, they will start with a function y = x2 - 9x + 1, highlight the first two terms, sketch that function using dashed lines, and then sketch in the "real" final function using solid line. They will repeat this a few times with different functions, until they can fluidly graph any y = ax2 + bx + c function. On this day, they'll also learn to visualize the axis of symmetry and to write its equation by inspection of graph.
Day 7: Going backwards from a graph to an equation
Plan - In pairs, they will be given one quadratic graph with two "nice", symmetric integer points being emphasized on the graph, one of the points being on the y-axis. They will be asked to sketch using dashed lines what this function would look like if you shifted those two points down to the x-axis, and be asked to write the function equation of both graphs. They will practice this a few times.
At the end of Day 7, they will be given a quadratic graph whose two "nice", symmetric integer points are both not on the y-axis. This tests them to see if they can figure out that the translated graph would have an equation that looks like y = (x - m)(x - n) + p instead of y = x(x - n) + p
Day 8: Playing around with the idea of adjusting "a".
Plan - In pairs, they will import Dan Meyer's basketball photo into GeoGebra. We will discuss as a class the need to find a modeling equation in order to fully predict whether the ball will make it into the hoop. From there, they will choose two nice integer points, write the equation, and graph. If they notice that the curve goes through those two points but doesn't have the correct steepness desired in order to fit the photo, then they will create a slider value in GeoGebra and toggle the value of "a" until they get a good "fit" around the graph, and record their results.
As a class, we will then go over the idea of solving for "a" using an unused point (x, y) and link it to solving for the y-intercept in linear functions. They will solve for "a" this way to compare analytical results against the technology results.
Day 9: Modeling Individually
Plan - Following a discussion of examples of parabolic applications, each pair will find and import their own photos of "real-life" parabolic shapes from the web. They will then model the function in Geogebra both using technology and using algebraic analysis.
Day 10: Creating posters
Plan - Each pair will create two posters, one with the modeled functions overlaying the photos, and one poster explaining the general process of graphing y = ax2 + bx + c and the general process of fitting an equation to a parabolic graph.
Day 11: Practice presentations
Day 12: Math fair for other classes / parents?!
Wednesday, April 17, 2013
Totally Silly but Works
I made up a totally silly call-and-response thing this year for practicing exponent rules (after we did the initial exploration, obviously, so that they could understand why the rules work). It's mad cheesy, but the kids totally remember the rules now!! The hardest part is keeping the clapping going, but I'm not sure if it's because of my students being totally off-rhythm in general or what (they're super suburban kids).
So we clap, step from side to side, and I say, "8B, are you ready?" and they chant, "Yeah, oh yeah!"
And then I call on a random kid, "Nora, are you ready?" and she chants, "Yeah, oh yeah!"
and then I call out one of the following: "Power times power", "Power to a power", or "Power over power" while holding up fingers in each hand (up to 5, obviously, in each hand) to represent the original exponents we're working with.
Depending on which one I call out, the kids need to reply with, "You gotta add them up!" "You gotta mul-ti-ply!" or "You gotta can-cel out!" in a sing-song voice, and that kid I named would then have to say the answer (resulting exponent) immediately after. (For example, if I am holding up 3 fingers and 5 fingers, and it's "power times power, you gotta add them up!" then the kid would shout out "8!")
And then we'd resume with me calling on the next kid randomly. It's mad cheesy, but it works! Afterwards, they were all loose and happy when practicing exponent rules. Every practice problem I would put on the board, I'd ask them which rule can be applied first or next, and they'd say it back in that sing-song voice, "you gotta mul-ti-ply!"
Go kids for being good sports!! It helps to make a boring topic a little less tedious! Next year, I'll necessarily add dance moves to help our kinesthetic learners. (I already have them. I came up with them after we did the exercise.)
Yup... I've got little shame left. :)
So we clap, step from side to side, and I say, "8B, are you ready?" and they chant, "Yeah, oh yeah!"
And then I call on a random kid, "Nora, are you ready?" and she chants, "Yeah, oh yeah!"
and then I call out one of the following: "Power times power", "Power to a power", or "Power over power" while holding up fingers in each hand (up to 5, obviously, in each hand) to represent the original exponents we're working with.
Depending on which one I call out, the kids need to reply with, "You gotta add them up!" "You gotta mul-ti-ply!" or "You gotta can-cel out!" in a sing-song voice, and that kid I named would then have to say the answer (resulting exponent) immediately after. (For example, if I am holding up 3 fingers and 5 fingers, and it's "power times power, you gotta add them up!" then the kid would shout out "8!")
And then we'd resume with me calling on the next kid randomly. It's mad cheesy, but it works! Afterwards, they were all loose and happy when practicing exponent rules. Every practice problem I would put on the board, I'd ask them which rule can be applied first or next, and they'd say it back in that sing-song voice, "you gotta mul-ti-ply!"
Go kids for being good sports!! It helps to make a boring topic a little less tedious! Next year, I'll necessarily add dance moves to help our kinesthetic learners. (I already have them. I came up with them after we did the exercise.)
Yup... I've got little shame left. :)
Wednesday, February 20, 2013
Visualizing Concepts
Here is an MS update. I feel pretty productive lately, as I always do during the second semester. I also feel quite productive with my Grade 11s, and as a result I'm taking on three new kids potentially, at least for a while. Grade 12's are doing OK, but the pressure is sure ramping up for their IB exams, so there's not a whole lot of "cool" instructional things that I can be doing with them...
Grade 8:
Referring to the system {5u + v = 21, 10u + 3v = 48}, one middle-of-the-road kid explained excitedly to her friend, "Oh! I got it! If 5u + v = 21, then 10u + 2v must equal 42. If you put that here into the second equation, then you will still have 1v on the left side. Which means that 42 + v = 48, and v must equal 6!"
Not bad for being day 1 of systems algebra. (Of course, they've been doing the same reasoning using shapes and visual substitution for several days now, so the transition to symbols was seamless. I didn't bother with even any examples on the board this year, and it worked out just fine without one.)
I went up to a boy who was one worksheet ahead, and pointed at the equation {y + 6x = 10,
y + 2x = 2} to ask him what immediate conclusion he could draw based on inspection. He immediately said, "X is 10 minus 2, divided by 4." I had to backtrack to ask him, "How do you know? Because 8 is equal to....?"
He finished my sentence, "4x." Great, now we're talking about the process.
I showed him the traditional notation for showing that work / reasoning via elimination, even though I know that in his head he's doing substitution from one (smaller) equation into the other.
y + 6x = 10
-(y + 2x = 2)
4x = 8
He was not impressed, nor surprised. When you introduce systems via pictures, the symbols become just part of the bigger concept. I explained to him that on the previous worksheet, I had let them just do much of it in their heads, but now we're going to work on the written communication piece, to carefully show our work on paper. I also gave him the hint that sometimes, instead of subtracting the smaller equation, he'll notice that he wants to add the equations instead. I said that he'll know when addition is necessary, because those equations will just "feel different." I left him on just that hint, and sure enough, 20 or so minutes later, when I came back, he had already identified the equations that needed to be added, and he was ruminating over the explicit mathematical reasons why that works. At that point, I felt that he was ready to discuss that if you have additive inverses, then you can just add them to cancel them, so we had a 1-minute discussion about that and I left him again.
I am very pleased with how this unit is going. I think I've gotten it down pretty pat; if I remember correctly, last year I didn't have to change any worksheets at all, and so far I haven't had to alter any worksheet either. This is one unit where I can just sit back and watch the kids' thinking unfold, more or less, and I can be very hands-off in their own building of the concepts of algebraic substitution and elimination. At some point, I looked around the room when I noticed the noise level rise, and saw that it was because literally every pair of kids is engaged in some sort of intense mathematical discussion with their neighbor. Awesome-o!
Grade 9:
In Grade 9, we've been working on learning / understanding / memorizing geometry area formulas via cutting and pasting. We each re-arranged, glued down a parallelogram to form a rectangle, to help them understand why A=bh for a parallelogram. Then, we each re-arranged a trapezoid into a thin parallelogram, to help them understand why A=(b1+b2)(h/2) for a trapezoid. This year, I went a step further and highlighted the base 1 and base 2 sides using a green marker, so that the kids can see that they line up within the parallelogram when we do a "move and flip" of the top half of the trapezoid. This simple highlighting technique is superbly visual for my visual learners to see why the new parallelogram base MUST be (b1+b2).
Then, I proceeded to give them two practice trapezoid problems. In both cases, I had them draw out the parallelogram that it becomes, labeling the side lengths to emphasize the numerical connection between the trapezoid and its resulting parallelogram. It worked great! My concrete thinkers really latched on after the first example. One of the weakest kids in my class went up to the board and bravely (and correctly) drew out the trapezoid, its new parallelogram dimensions, and the calculated area, without any previous verification that he was on track. I was proud!!
I just love geometry lessons like this, because they involve both tactile and visual learners and help the concept "stick" in their heads. Slowly, I'm getting their geometry concepts up and running in order to do the 3-D project this year.
Addendum March 4, 2013: Here is a visual that Lara has made on Pinterest. Thanks, Lara!
Grade 7:
In Grade 7, we've also been doing Geometry... I'll have to report on that at another time, but I wanted to say that recently (prior to the Geometry unit), I discovered the best technique for teaching setting up of proportions. For ages it used to bother me that kids would not check that two ratios have matching units across the numerators (and across the denominators), and so half the time they would set up incorrect proportions. I figured out a trick this year. The first day we learned to set up proportions, I had them highlight the matching units across the equal sign. For that whole first day, they had to always highlight the units inside the proportions, and check that the matching colors lined up horizontally. After that first day, the highlighters went away and I never referred to them again. In the end, I didn't have a single kid mix up the positions of the numbers inside the proportions on the test. I think that mentally, the colors stuck with them and they're always visualizing that check, even when the highlighters aren't around anymore.
Again, slowing the kids down in the beginning definitely pays off, I think. The highlighters are a trick that I'm trying to use more and more, to incorporate hidden visualization techniques that some of us "math people" tend to internalize in our minds but that teenagers who are used to rushing through things, could need more explicit instruction on. So far, so good.
Grade 8:
Referring to the system {5u + v = 21, 10u + 3v = 48}, one middle-of-the-road kid explained excitedly to her friend, "Oh! I got it! If 5u + v = 21, then 10u + 2v must equal 42. If you put that here into the second equation, then you will still have 1v on the left side. Which means that 42 + v = 48, and v must equal 6!"
Not bad for being day 1 of systems algebra. (Of course, they've been doing the same reasoning using shapes and visual substitution for several days now, so the transition to symbols was seamless. I didn't bother with even any examples on the board this year, and it worked out just fine without one.)
I went up to a boy who was one worksheet ahead, and pointed at the equation {y + 6x = 10,
y + 2x = 2} to ask him what immediate conclusion he could draw based on inspection. He immediately said, "X is 10 minus 2, divided by 4." I had to backtrack to ask him, "How do you know? Because 8 is equal to....?"
He finished my sentence, "4x." Great, now we're talking about the process.
I showed him the traditional notation for showing that work / reasoning via elimination, even though I know that in his head he's doing substitution from one (smaller) equation into the other.
y + 6x = 10
-(y + 2x = 2)
4x = 8
He was not impressed, nor surprised. When you introduce systems via pictures, the symbols become just part of the bigger concept. I explained to him that on the previous worksheet, I had let them just do much of it in their heads, but now we're going to work on the written communication piece, to carefully show our work on paper. I also gave him the hint that sometimes, instead of subtracting the smaller equation, he'll notice that he wants to add the equations instead. I said that he'll know when addition is necessary, because those equations will just "feel different." I left him on just that hint, and sure enough, 20 or so minutes later, when I came back, he had already identified the equations that needed to be added, and he was ruminating over the explicit mathematical reasons why that works. At that point, I felt that he was ready to discuss that if you have additive inverses, then you can just add them to cancel them, so we had a 1-minute discussion about that and I left him again.
I am very pleased with how this unit is going. I think I've gotten it down pretty pat; if I remember correctly, last year I didn't have to change any worksheets at all, and so far I haven't had to alter any worksheet either. This is one unit where I can just sit back and watch the kids' thinking unfold, more or less, and I can be very hands-off in their own building of the concepts of algebraic substitution and elimination. At some point, I looked around the room when I noticed the noise level rise, and saw that it was because literally every pair of kids is engaged in some sort of intense mathematical discussion with their neighbor. Awesome-o!
Grade 9:
In Grade 9, we've been working on learning / understanding / memorizing geometry area formulas via cutting and pasting. We each re-arranged, glued down a parallelogram to form a rectangle, to help them understand why A=bh for a parallelogram. Then, we each re-arranged a trapezoid into a thin parallelogram, to help them understand why A=(b1+b2)(h/2) for a trapezoid. This year, I went a step further and highlighted the base 1 and base 2 sides using a green marker, so that the kids can see that they line up within the parallelogram when we do a "move and flip" of the top half of the trapezoid. This simple highlighting technique is superbly visual for my visual learners to see why the new parallelogram base MUST be (b1+b2).
Then, I proceeded to give them two practice trapezoid problems. In both cases, I had them draw out the parallelogram that it becomes, labeling the side lengths to emphasize the numerical connection between the trapezoid and its resulting parallelogram. It worked great! My concrete thinkers really latched on after the first example. One of the weakest kids in my class went up to the board and bravely (and correctly) drew out the trapezoid, its new parallelogram dimensions, and the calculated area, without any previous verification that he was on track. I was proud!!
I just love geometry lessons like this, because they involve both tactile and visual learners and help the concept "stick" in their heads. Slowly, I'm getting their geometry concepts up and running in order to do the 3-D project this year.
Addendum March 4, 2013: Here is a visual that Lara has made on Pinterest. Thanks, Lara!
Grade 7:
In Grade 7, we've also been doing Geometry... I'll have to report on that at another time, but I wanted to say that recently (prior to the Geometry unit), I discovered the best technique for teaching setting up of proportions. For ages it used to bother me that kids would not check that two ratios have matching units across the numerators (and across the denominators), and so half the time they would set up incorrect proportions. I figured out a trick this year. The first day we learned to set up proportions, I had them highlight the matching units across the equal sign. For that whole first day, they had to always highlight the units inside the proportions, and check that the matching colors lined up horizontally. After that first day, the highlighters went away and I never referred to them again. In the end, I didn't have a single kid mix up the positions of the numbers inside the proportions on the test. I think that mentally, the colors stuck with them and they're always visualizing that check, even when the highlighters aren't around anymore.
Again, slowing the kids down in the beginning definitely pays off, I think. The highlighters are a trick that I'm trying to use more and more, to incorporate hidden visualization techniques that some of us "math people" tend to internalize in our minds but that teenagers who are used to rushing through things, could need more explicit instruction on. So far, so good.
Wednesday, January 30, 2013
Grade 9 Videos Review Project
I am learning from a not-great experience with having kids create videos to recap the skills that we had learned during the first semester. I'm jotting it down here so that you can read about how it went and help me to make it better next time.
I still think the idea was good. We had done so much great multi-stepped, contextual algebra practice during the first semester (with my "low" Grade 9 class), that I didn't want them to just leave it all behind as we move on to new Geometry topics in the second semester. I didn't want to have to come back in June to re-teach them everything they knew, but I knew that retention would always be a problem for these kids.
So, I came up with the idea that we'd divvy up all the topics from the first semester, and each group would be responsible to make some explanatory videos on one topic. They'd upload the videos to the web, and I would provide links for all the kids to access these instructional videos. Then, during Spring Break, I'd assign as vacation homework for the kids to watch each other's videos and to do just two or so practice problems related to each video. This way, they're somewhat refreshed on the old concepts over time, and it also takes the pressure off of me as the "all-knowing info source" when it comes to review time.
Sounds good in theory, except I totally underestimated what a huuuuge task this would be for a group of kids who cannot really self-monitor their progress very effectively. They really did try; that I am impressed by. I had helped them prepare for the filming last week prior to leaving for the AGIS Conference, in hopes that they could just use my day of absence to film their videos on the iPads and to upload them. Little did I know that it was not going to be so easy. When I got back this week and looked at the videos, I was pretty disappointed. Most of their videos either had inaccurate mathematics, or the problems they picked were too easy (or, sometimes, too ambitious). I blame that on myself; if you want it to be done right, you simply have to closely supervise the kids in order to give them just-in-time feedback as they are filming and pulling those last pieces together. So, today in class I gave them another 80 minutes to re-do and re-do their mathematics and their videos. This time, I checked in with every group to make sure that their math was production-ready by the time they started filming. Even then, they still had to repeat the filming a bunch of times just to avoid all the careless mistakes. It was just so tough for them to master the simultaneous communication and solving of a multi-stepped problem. In the end, it was really good practice for them to zoom in on their own mistakes and to keep re-doing to correct them, even though the final video quality was not great. (On the iPads, the audio and the video are both of weak quality.) Fortunately, since the kids had mostly selected (with my help) the topics that they had individually struggled with on the semester test, this was a great remediation strategy for them to have to create these explanatory videos, regardless of video quality.
In the future, I really need to think carefully about what technology to use, how to set up the room so that different groups can be filming at the same time, how to help them rehearse prior to filming, etc. There is too big of a range between groups who put in a lot of effort into this project to make a good video, and those who just kind of slapped something together and called it a day. I also need to think about the timing, because unfortunately, this project takes too much time in class, as the kids need support all the way through (including the filming parts) and part of me just wants to move on to new topics already, knowing how much ground we still have to cover.
It's quite a shame that this project didn't work out to have superb products, because I think the process was definitely worthwhile and many of the kids learned a fair amount while doing this. It was definitely challenging for them, and I think some of their frustration came from how challenging this task was. I have hope though, that with some restructuring, I can find a way to make this work much better the next time. One of the restructuring ideas I had, for example, was that instead of everyone doing review videos all at once after a whole semester, after each unit I'd pick a small group of students (who had performed weakly on the exam) to do the videos for just that recent topic. This will ensure that timing is less of an issue, because they'd just work on it outside of class with my help, say at lunch time, and it'd also ensure more immediate remediation. I would also be able to ensure the videos are of better quality, since I am only focusing on managing one group at a time. Have you ever done something like this? Can you share any tips with me to make this a more successful experience in the future?
Addendum: Here are a few samples of produced videos. http://bit.ly/linesReview1, http://bit.ly/linesReview2, http://bit.ly/linesReview3, http://bit.ly/anglesReview1, http://bit.ly/anglesReview2. The kids in my "low" group had to create videos for lines, quadratics, midpoint/distance word problems, drawing geometric diagrams, and analysis of angles. Blip.tv only lets me upload 3 videos each day, so I'll post more links later!
I still think the idea was good. We had done so much great multi-stepped, contextual algebra practice during the first semester (with my "low" Grade 9 class), that I didn't want them to just leave it all behind as we move on to new Geometry topics in the second semester. I didn't want to have to come back in June to re-teach them everything they knew, but I knew that retention would always be a problem for these kids.
So, I came up with the idea that we'd divvy up all the topics from the first semester, and each group would be responsible to make some explanatory videos on one topic. They'd upload the videos to the web, and I would provide links for all the kids to access these instructional videos. Then, during Spring Break, I'd assign as vacation homework for the kids to watch each other's videos and to do just two or so practice problems related to each video. This way, they're somewhat refreshed on the old concepts over time, and it also takes the pressure off of me as the "all-knowing info source" when it comes to review time.
Sounds good in theory, except I totally underestimated what a huuuuge task this would be for a group of kids who cannot really self-monitor their progress very effectively. They really did try; that I am impressed by. I had helped them prepare for the filming last week prior to leaving for the AGIS Conference, in hopes that they could just use my day of absence to film their videos on the iPads and to upload them. Little did I know that it was not going to be so easy. When I got back this week and looked at the videos, I was pretty disappointed. Most of their videos either had inaccurate mathematics, or the problems they picked were too easy (or, sometimes, too ambitious). I blame that on myself; if you want it to be done right, you simply have to closely supervise the kids in order to give them just-in-time feedback as they are filming and pulling those last pieces together. So, today in class I gave them another 80 minutes to re-do and re-do their mathematics and their videos. This time, I checked in with every group to make sure that their math was production-ready by the time they started filming. Even then, they still had to repeat the filming a bunch of times just to avoid all the careless mistakes. It was just so tough for them to master the simultaneous communication and solving of a multi-stepped problem. In the end, it was really good practice for them to zoom in on their own mistakes and to keep re-doing to correct them, even though the final video quality was not great. (On the iPads, the audio and the video are both of weak quality.) Fortunately, since the kids had mostly selected (with my help) the topics that they had individually struggled with on the semester test, this was a great remediation strategy for them to have to create these explanatory videos, regardless of video quality.
In the future, I really need to think carefully about what technology to use, how to set up the room so that different groups can be filming at the same time, how to help them rehearse prior to filming, etc. There is too big of a range between groups who put in a lot of effort into this project to make a good video, and those who just kind of slapped something together and called it a day. I also need to think about the timing, because unfortunately, this project takes too much time in class, as the kids need support all the way through (including the filming parts) and part of me just wants to move on to new topics already, knowing how much ground we still have to cover.
It's quite a shame that this project didn't work out to have superb products, because I think the process was definitely worthwhile and many of the kids learned a fair amount while doing this. It was definitely challenging for them, and I think some of their frustration came from how challenging this task was. I have hope though, that with some restructuring, I can find a way to make this work much better the next time. One of the restructuring ideas I had, for example, was that instead of everyone doing review videos all at once after a whole semester, after each unit I'd pick a small group of students (who had performed weakly on the exam) to do the videos for just that recent topic. This will ensure that timing is less of an issue, because they'd just work on it outside of class with my help, say at lunch time, and it'd also ensure more immediate remediation. I would also be able to ensure the videos are of better quality, since I am only focusing on managing one group at a time. Have you ever done something like this? Can you share any tips with me to make this a more successful experience in the future?
Addendum: Here are a few samples of produced videos. http://bit.ly/linesReview1, http://bit.ly/linesReview2, http://bit.ly/linesReview3, http://bit.ly/anglesReview1, http://bit.ly/anglesReview2. The kids in my "low" group had to create videos for lines, quadratics, midpoint/distance word problems, drawing geometric diagrams, and analysis of angles. Blip.tv only lets me upload 3 videos each day, so I'll post more links later!
Tuesday, January 15, 2013
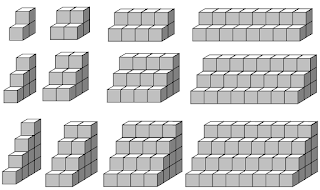
Visual pattern of 3 variables
Since I have multi-input relationships on my mind, here is a visual pattern of 3 variables for you to enjoy (row, column, result). I've submitted this to the good folks at visualpatterns.org, but because of the nature of the complexity of this problem, I'm not quite sure that it quite fits well with everything else over there. Anyhow, it's a good problem for your abstract thinkers and ties in the concept of both arithmetic and geometric sequences quite nicely, I think.
Above shows rows 1, 2, 3 starting at the top. It also shows columns 1, 2, 3, 4 starting from the left to the right. At this rate, in row 8, column 10, there will be 23040 cubes. Can you find out how many cubes there will be for row 20, column 15?
Above shows rows 1, 2, 3 starting at the top. It also shows columns 1, 2, 3, 4 starting from the left to the right. At this rate, in row 8, column 10, there will be 23040 cubes. Can you find out how many cubes there will be for row 20, column 15?
Friday, January 11, 2013
3-Variable Project Success!
This is a follow up to my three-variable project in Grade 8, which we're finally doing now that the semester test is out of the way. The kids are really enjoying it, and it helps to solidify the idea that multiple variables can cause the numerical output to change. (I tied this in our introductory discussion to familiar formulas like A=lw and P=2l + 2w). Prior to starting the project, I also quickly pulled up a real-world 3-variable table and asked them to tell me where the causes are and where the effects are, inside this format of the stockings sizing chart. This really helped them to understand and relate to the table setup on their given project sheet, in terms of visualizing why the table is set up that way.
They worked through the first table with guidance, and found the general formula pretty easily once I asked them "if n = 100, what is the formula for y? What if n = 372? What if n is just any n?" After this, they repeated the process for the second (and for some students, as well the third) table of values. The last two days we worked on verifying the general formulas they found, first manually -- learning to show proper work for multiple math test cases -- then with technology.
It took me a little bit to figure out how to set this up, but I made this http://bit.ly/excelTestTemplate to help my 8th-graders test their general formulas for their projects. I am very excited to see the outcome of this project, because as part of the testing procedure I also taught them how to program a very basic loop in the graphing calculator, in order to prompt for two variables, perform a basic formula, and then output the results. It looks like this for testing the first formula y = mn + n.
:While 1
:Prompt M
:Prompt N
:Disp M*N + N
:End
The kids took about 30 minutes today programming their graphing calcs to run their general formulas, testing them with a few entries from the table, and documenting it all using their camera phones in order to insert it into the math reports that they will be working all of next week. SWEETNESS. This'll be their second time writing a formal Grade 8 math paper for me, and since the first ones were pretty decent, I think this round will be as well.
I also made this project writeup guidelines to help them with framing their writeup. We discussed at various points of this project, how this mathematical process is very similar to the scientific process, with looking at the effect of a single variable at a time, then combining results to form a general hypothesis (ie. the general formula involving all variables), then test-test-testing your hypothesis using a variety of test cases and test methods. What a perfect age group to do this with, since their little minds are just opening up to the world of thinking logically and sequentially and doubting everything.
I hope you have a break in between heavy-duty algebra topics to do this with your kids. Highly recommended! Super duper multi-faceted project involving a variety of skills.
Addendum: My colleague recommended to me that at the end of the project, I show the kids the 3-D graph using x, y, z as the variables. Wow, that's pretty crazy. I don't know if they're quite ready to handle this!
They worked through the first table with guidance, and found the general formula pretty easily once I asked them "if n = 100, what is the formula for y? What if n = 372? What if n is just any n?" After this, they repeated the process for the second (and for some students, as well the third) table of values. The last two days we worked on verifying the general formulas they found, first manually -- learning to show proper work for multiple math test cases -- then with technology.
It took me a little bit to figure out how to set this up, but I made this http://bit.ly/excelTestTemplate to help my 8th-graders test their general formulas for their projects. I am very excited to see the outcome of this project, because as part of the testing procedure I also taught them how to program a very basic loop in the graphing calculator, in order to prompt for two variables, perform a basic formula, and then output the results. It looks like this for testing the first formula y = mn + n.
:While 1
:Prompt M
:Prompt N
:Disp M*N + N
:End
The kids took about 30 minutes today programming their graphing calcs to run their general formulas, testing them with a few entries from the table, and documenting it all using their camera phones in order to insert it into the math reports that they will be working all of next week. SWEETNESS. This'll be their second time writing a formal Grade 8 math paper for me, and since the first ones were pretty decent, I think this round will be as well.
I also made this project writeup guidelines to help them with framing their writeup. We discussed at various points of this project, how this mathematical process is very similar to the scientific process, with looking at the effect of a single variable at a time, then combining results to form a general hypothesis (ie. the general formula involving all variables), then test-test-testing your hypothesis using a variety of test cases and test methods. What a perfect age group to do this with, since their little minds are just opening up to the world of thinking logically and sequentially and doubting everything.
I hope you have a break in between heavy-duty algebra topics to do this with your kids. Highly recommended! Super duper multi-faceted project involving a variety of skills.
Addendum: My colleague recommended to me that at the end of the project, I show the kids the 3-D graph using x, y, z as the variables. Wow, that's pretty crazy. I don't know if they're quite ready to handle this!
Saturday, December 8, 2012
11 Recommendations to Middle-ish Grades Math Teachers
Maybe some of these are "radical" and "offensive", or maybe they're not. I'm just throwing them out there. Please don't hate me if you do some of these (I know a couple of them are quite commonly done by many math teachers). These are just my personal opinions, but I feel quite strongly about them. I figured I'd say it here, because some of these things drive me nuts, and I need an outlet.
11. Do not tell a kid to "move things across the equal sign and just change the signs". Preferably you don't ever say this phrase to a kid ever, but if a kid comes to you and says that someone else somewhere (ie. a parent or another teacher) has taught that to them, you need to drill into them the reason why this shortcut works. Grill them until they can articulate why the term necessarily shows up on the other side with the opposite sign.
Reason: If you teach shortcuts like this without the correct foundation of understanding, then down the road the kid cannot approach a complex situation intuitively, because they cannot visualize the equation as a balance.
10. Do not allow your students to do simple equations only in their heads / showing little or no work at the early stages.
Reason: Even if the kid is bright and they can do the equation correctly every time, you are helping them to develop a bad habit that is hard to break. Down the road, when the equations get more complicated and the kid starts to make procedural mistakes, they'll have such a hard time finding their mistakes because they've habitually skipped so many steps.
9. Do not allow your students to "open parentheses" without knowing why they do this and where it is the most useful.
Reason: Normally, it just irks me to see kids do 2(3 - 5 + 1) = 6 - 10 + 2 = -2 instead of following PEMDAS to do 2(3 - 5 + 1) = 2(-1) = -2, but it's really feckin' scary when I see students do
2 (4·5 + 7) = 8 + 10 + 14 = 32 in their second year of algebra. When all the values are known, they don't need to be distributing!!
8. Do not introduce integer operations without explaining the meaning of addition and subtraction of signed numbers! You can use number lines or you can use the idea of counting and neutralizing terms, but in the end, the kids need a framework of understanding.
Reason: I recently tutored a kid on a one-time basis (I was doing a favor for her parent, who's my friend, even though the kid doesn't go to our school), and the kid only knows memorized rules (she rattled them off like a poem), with no conceptual understanding whatsoever when I probed further. Unfortunately, that kind of problem is not really fixable in a day. It can take a teacher weeks to instill the correct habit of thinking. If you teach a kid to memorize a rule for adding or subtracting integers without understanding, then I can almost guarantee you that after the summer they won't remember it. And, if you first teach the rules by memorization, even if you try to explain afterwards the conceptual reasons for the rules, there ain't no one listening.
7. Do not teach "rise over run".
Reason: In my experience, a majority of the concrete-thinking kids out there do not know what the slope means. When you ask them, they just enthusiastically say "rise over run", but they cannot identify it in a table, they cannot find it in a word problem, they certainly cannot say that it's change of y over change of x, and half of them cannot even see it in a graph.
You have other alternatives. I teach slope as "what happens (with the quantity we care about), over how long it takes." For example, the speed of a car is "miles, per hour"; the rate of growth of a plant is "inches, per number of days"; the rate of decrease of savings can be "dollars, per number of weeks". You have alternatives to "rise over run". Learn to teach kids to visualize the coordinate plane as a sort of timeline, where the y-axis describes the interesting values we are observing, and x-axis describes the stages at which those values occur. Once they understand this, then they can correctly pick out the slope given any representation of the function.
6. Do not let any kid in your class get away with saying "A linear function is something that is
y = mx + b."
Reason: Again, in my experience, I can habitually meet a full class of kids who had spent a good part of a previous year learning about lines and linear equations and linear operations, and in the following year when they move to my class and I ask them to tell me simply what is a linear function, the only thing they can say is: Y = mx + b. That is really, really bad. The first thing they should be able to say is that it is a straight line, or that it is a pattern with a constant rate.
Please, please, do teach lines in context. Make sure that kids know what y, m, x, and b all mean in a simple linear situation.
5. Do not introduce sine, cosine, and tangent without explaining their relationship to similar triangles.
Reason: The concept is too abstract, too much of a jump from anything else the kids have done. Give the kids some shadow problems to allow them to see what the ancient mathematicians saw, and why they recorded trigonometric ratios in a chart. Let the 3 ratios arise as an outcome of a natural discovery, a natural need. And then, when you introduce the terms sine, cosine, and tangent, the kids will at least already understand them as sweet nicknames for comparisons between sides.
From then on, whenever you say sin(x) = 0.1283... , remind kids what that means simply by immediately saying, "So the opposite side is about 12.8% as long as the hypotenuse." If you do this consistently, kids will never grow afraid of those ratios.
4. Do not teach right-triangle trigonometry from inside the classroom!
Reason: Kids need to be able to visualize geometry relationships, especially in word problems. Some kids have trouble doing this on a flat sheet of paper. Don't disadvantage those learners. Take them outside, make them build an inclinometer, make them experience angles of elevation, angles of depression, and the idea of measuring heights through triangular ratios. This really only takes a day, or at most two. In the end, when you take them back to the classroom, you will be amazed at how well they can now visualize even complicated word problems involving multiple right triangles.
3. Do distinguish between conceptual and procedural errors. Your modes of intervention should look very different for those two types of mistakes, and what you communicate to the kids as recommended "next steps" should look fairly different as well.
2. Do incorporate writing into your classroom. Writing is an extremely valuable way of learning mathematics. Every project should have a significant writing component. When kids write, they are forced to engage with the subject on a personal level, and so they learn much more.
1. Do make learning fun. From a biological perspective (of primitive survival), our brain makes us remember things permanently when our emotions are triggered. Fun learning isn't a waste of time. It's necessary to help the students build long-term memory!
11. Do not tell a kid to "move things across the equal sign and just change the signs". Preferably you don't ever say this phrase to a kid ever, but if a kid comes to you and says that someone else somewhere (ie. a parent or another teacher) has taught that to them, you need to drill into them the reason why this shortcut works. Grill them until they can articulate why the term necessarily shows up on the other side with the opposite sign.
Reason: If you teach shortcuts like this without the correct foundation of understanding, then down the road the kid cannot approach a complex situation intuitively, because they cannot visualize the equation as a balance.
10. Do not allow your students to do simple equations only in their heads / showing little or no work at the early stages.
Reason: Even if the kid is bright and they can do the equation correctly every time, you are helping them to develop a bad habit that is hard to break. Down the road, when the equations get more complicated and the kid starts to make procedural mistakes, they'll have such a hard time finding their mistakes because they've habitually skipped so many steps.
9. Do not allow your students to "open parentheses" without knowing why they do this and where it is the most useful.
Reason: Normally, it just irks me to see kids do 2(3 - 5 + 1) = 6 - 10 + 2 = -2 instead of following PEMDAS to do 2(3 - 5 + 1) = 2(-1) = -2, but it's really feckin' scary when I see students do
2 (4·5 + 7) = 8 + 10 + 14 = 32 in their second year of algebra. When all the values are known, they don't need to be distributing!!
8. Do not introduce integer operations without explaining the meaning of addition and subtraction of signed numbers! You can use number lines or you can use the idea of counting and neutralizing terms, but in the end, the kids need a framework of understanding.
Reason: I recently tutored a kid on a one-time basis (I was doing a favor for her parent, who's my friend, even though the kid doesn't go to our school), and the kid only knows memorized rules (she rattled them off like a poem), with no conceptual understanding whatsoever when I probed further. Unfortunately, that kind of problem is not really fixable in a day. It can take a teacher weeks to instill the correct habit of thinking. If you teach a kid to memorize a rule for adding or subtracting integers without understanding, then I can almost guarantee you that after the summer they won't remember it. And, if you first teach the rules by memorization, even if you try to explain afterwards the conceptual reasons for the rules, there ain't no one listening.
7. Do not teach "rise over run".
Reason: In my experience, a majority of the concrete-thinking kids out there do not know what the slope means. When you ask them, they just enthusiastically say "rise over run", but they cannot identify it in a table, they cannot find it in a word problem, they certainly cannot say that it's change of y over change of x, and half of them cannot even see it in a graph.
You have other alternatives. I teach slope as "what happens (with the quantity we care about), over how long it takes." For example, the speed of a car is "miles, per hour"; the rate of growth of a plant is "inches, per number of days"; the rate of decrease of savings can be "dollars, per number of weeks". You have alternatives to "rise over run". Learn to teach kids to visualize the coordinate plane as a sort of timeline, where the y-axis describes the interesting values we are observing, and x-axis describes the stages at which those values occur. Once they understand this, then they can correctly pick out the slope given any representation of the function.
6. Do not let any kid in your class get away with saying "A linear function is something that is
y = mx + b."
Reason: Again, in my experience, I can habitually meet a full class of kids who had spent a good part of a previous year learning about lines and linear equations and linear operations, and in the following year when they move to my class and I ask them to tell me simply what is a linear function, the only thing they can say is: Y = mx + b. That is really, really bad. The first thing they should be able to say is that it is a straight line, or that it is a pattern with a constant rate.
Please, please, do teach lines in context. Make sure that kids know what y, m, x, and b all mean in a simple linear situation.
5. Do not introduce sine, cosine, and tangent without explaining their relationship to similar triangles.
Reason: The concept is too abstract, too much of a jump from anything else the kids have done. Give the kids some shadow problems to allow them to see what the ancient mathematicians saw, and why they recorded trigonometric ratios in a chart. Let the 3 ratios arise as an outcome of a natural discovery, a natural need. And then, when you introduce the terms sine, cosine, and tangent, the kids will at least already understand them as sweet nicknames for comparisons between sides.
From then on, whenever you say sin(x) = 0.1283... , remind kids what that means simply by immediately saying, "So the opposite side is about 12.8% as long as the hypotenuse." If you do this consistently, kids will never grow afraid of those ratios.
4. Do not teach right-triangle trigonometry from inside the classroom!
Reason: Kids need to be able to visualize geometry relationships, especially in word problems. Some kids have trouble doing this on a flat sheet of paper. Don't disadvantage those learners. Take them outside, make them build an inclinometer, make them experience angles of elevation, angles of depression, and the idea of measuring heights through triangular ratios. This really only takes a day, or at most two. In the end, when you take them back to the classroom, you will be amazed at how well they can now visualize even complicated word problems involving multiple right triangles.
3. Do distinguish between conceptual and procedural errors. Your modes of intervention should look very different for those two types of mistakes, and what you communicate to the kids as recommended "next steps" should look fairly different as well.
2. Do incorporate writing into your classroom. Writing is an extremely valuable way of learning mathematics. Every project should have a significant writing component. When kids write, they are forced to engage with the subject on a personal level, and so they learn much more.
1. Do make learning fun. From a biological perspective (of primitive survival), our brain makes us remember things permanently when our emotions are triggered. Fun learning isn't a waste of time. It's necessary to help the students build long-term memory!
Saturday, November 17, 2012
Teaching Number Definitions Meaningfully
As a kid, I was never good with mathematical terms. I was always doodling in math class and only picked up vocabulary words osmotically (which also meant not so effectively). As a teacher, I have tried to make vocab instruction more meaningful for kids.
Recently, in Grade 8, we started talking about inequalities for the first time. I started off the discussion by asking kids to give me some examples of equalities, and we wrote them on the board. After a few minutes, we started to list examples of inequalities and I went over why in math, saying -5 is less than -2 is a bit more precise/less confusing than saying -5 is smaller than -2.
Then, I asked the kids to come up with some example numbers that can satisfy the inequality
x + 2 < 15 . The kids started to list numbers, and after a few minutes I asked them for what they wrote down, and in the context of this we discussed number types. I explained to them that I think generally, in life, when you want to brainstorm options in your head, you don't want to keep listing the same types of objects over and over again, because in doing so you are limiting your vision of what is possible. The examples that the first kid gave me were {1, 2, 3, ..... , 12} and the examples that the second kid gave me were {-1, -2, -3, -100}
I drew on the board this diagram and said that "a long time ago, when cave people started counting sticks on the ground, they came up with numbers like 1, 2, 3, 4... These were called natural numbers.* Then eventually they came up with one more number to add to that set, and they called it whole numbers. Can you guess what that new number was?"
After kids enthusiastically guessed zero, they were starting to understand this diagram representation of a subset and were beginning to appreciate the historical development of numbers. Then, I added another layer of negative numbers and asked them what that is called when we started at some point to include/consider negative numbers as well.
They figured out that it was called integers. Great!
Then, I asked them what types of numbers they still know / have learned that we haven't named yet. They gave examples of decimals and fractions, and we added them to this picture.
In the end, we went back to the original topic at hand of finding example numbers that satisfy the inequality x + 2 < 15, and this time they were much better equipped to list a variety of examples and to discuss the full range of (non-discrete) solutions, which then led to the discussion of shading the solutions on the number line, and why we need the open circle rather than the closed circle sometimes.
I find this to be a more natural way to teach number types. Another time when I have done this was in teaching 9th-graders how to think of possible counterexamples that might disprove a math statement. If in their heads they are only considering a single type of example, then they're not being effective and thorough in their consideration of possibilities. As a kid, I would have appreciated this type of instruction of categorical types, followed immediately by application of its usefulness, and it would have probably helped me remember the names better. So, for me as a teacher, I always think it is important that I don't introduce the number definitions purely in isolation just because it's part of section 1.1 in the textbook. In the end, our teaching of these numerical categories should be explicitly supporting the kids' thinking, rather than just to add to the volume of disconnected rote knowledge in their heads...
*Note: By the way, I prefer this definition of natural numbers, even though I know that mathematicians don't all agree. Some refer to zero as part of the natural number set.
Recently, in Grade 8, we started talking about inequalities for the first time. I started off the discussion by asking kids to give me some examples of equalities, and we wrote them on the board. After a few minutes, we started to list examples of inequalities and I went over why in math, saying -5 is less than -2 is a bit more precise/less confusing than saying -5 is smaller than -2.
Then, I asked the kids to come up with some example numbers that can satisfy the inequality
x + 2 < 15 . The kids started to list numbers, and after a few minutes I asked them for what they wrote down, and in the context of this we discussed number types. I explained to them that I think generally, in life, when you want to brainstorm options in your head, you don't want to keep listing the same types of objects over and over again, because in doing so you are limiting your vision of what is possible. The examples that the first kid gave me were {1, 2, 3, ..... , 12} and the examples that the second kid gave me were {-1, -2, -3, -100}
I drew on the board this diagram and said that "a long time ago, when cave people started counting sticks on the ground, they came up with numbers like 1, 2, 3, 4... These were called natural numbers.* Then eventually they came up with one more number to add to that set, and they called it whole numbers. Can you guess what that new number was?"
After kids enthusiastically guessed zero, they were starting to understand this diagram representation of a subset and were beginning to appreciate the historical development of numbers. Then, I added another layer of negative numbers and asked them what that is called when we started at some point to include/consider negative numbers as well.
They figured out that it was called integers. Great!
Then, I asked them what types of numbers they still know / have learned that we haven't named yet. They gave examples of decimals and fractions, and we added them to this picture.
In the end, we went back to the original topic at hand of finding example numbers that satisfy the inequality x + 2 < 15, and this time they were much better equipped to list a variety of examples and to discuss the full range of (non-discrete) solutions, which then led to the discussion of shading the solutions on the number line, and why we need the open circle rather than the closed circle sometimes.
I find this to be a more natural way to teach number types. Another time when I have done this was in teaching 9th-graders how to think of possible counterexamples that might disprove a math statement. If in their heads they are only considering a single type of example, then they're not being effective and thorough in their consideration of possibilities. As a kid, I would have appreciated this type of instruction of categorical types, followed immediately by application of its usefulness, and it would have probably helped me remember the names better. So, for me as a teacher, I always think it is important that I don't introduce the number definitions purely in isolation just because it's part of section 1.1 in the textbook. In the end, our teaching of these numerical categories should be explicitly supporting the kids' thinking, rather than just to add to the volume of disconnected rote knowledge in their heads...
*Note: By the way, I prefer this definition of natural numbers, even though I know that mathematicians don't all agree. Some refer to zero as part of the natural number set.
Friday, November 16, 2012
Three-Variable Investigation... in Grade 8!
Even after teaching all of grades 7 through 12, I still LOVE teaching 8th-graders the best. (This is my 5th year teaching 8th-graders.) They have just accumulated enough algebra under their belts to be able to do rich explorations, and they are still so naturally curious about the world. They are like math ninjas, always ready to pull out their math skills to apply to the world at a short notice, and never intimidated by the look of a problem.
In the past couple of years, I realized that it's a real shame that we don't do modeling with three variables in middle-school math. It's a shame because it would be such a terrific tie in to the scientific process, to show how in mathematics you can also hold one variable constant while examining the effect of another variable on the output, and vice versa, and then in the end generalize the results into one grand conclusion. (I realized this because, looking at the past IB portfolios, this is a required skill for 11th- and 12th- graders. This was news to me as a person coming from the American curriculum.)
This year, I decided that I will try to remedy this gaping hole in our curriculum by exposing my 8th-graders to a new assignment. Take a look! They will be completing parts of this at home, then bringing it to class for discussions as a group. And then they will take more of it home to do. Eventually, when all kids feel comfortable with the process and the results, they will write it up like a modeling report. (We have already written one lab report this year based on Dan's awesome activity, and they found it very challenging / a great learning experience. In that lab, they had to learn how to define variables, collect data, determine the type of regression, perform regression, interpret results, make mathematical predictions, test their prediction, and then do error analysis. We followed it up with a very rigorous write-up process that included carefully critiqued rough drafts and a day spent on discussing how to create / insert graphs using GeoGebra and how to structure their writeup in a logical sequence.) Since I am a firm believer that kids learn more through writing about their understanding, the gears in my head are already turning to think about this next modeling assignment.
Anyway, I am VERRRRY excited about this three-variable assignment. Since the topic is already abstract, I kept the patterns linear to make it more accessible to all kids. But, I am very hopeful that it could turn out to be an awesome learning experience.
Addendum: For you new readers, this analogy is what I am going to use to kick off the introduction of 3-variable relationships in the real world.
In the past couple of years, I realized that it's a real shame that we don't do modeling with three variables in middle-school math. It's a shame because it would be such a terrific tie in to the scientific process, to show how in mathematics you can also hold one variable constant while examining the effect of another variable on the output, and vice versa, and then in the end generalize the results into one grand conclusion. (I realized this because, looking at the past IB portfolios, this is a required skill for 11th- and 12th- graders. This was news to me as a person coming from the American curriculum.)
This year, I decided that I will try to remedy this gaping hole in our curriculum by exposing my 8th-graders to a new assignment. Take a look! They will be completing parts of this at home, then bringing it to class for discussions as a group. And then they will take more of it home to do. Eventually, when all kids feel comfortable with the process and the results, they will write it up like a modeling report. (We have already written one lab report this year based on Dan's awesome activity, and they found it very challenging / a great learning experience. In that lab, they had to learn how to define variables, collect data, determine the type of regression, perform regression, interpret results, make mathematical predictions, test their prediction, and then do error analysis. We followed it up with a very rigorous write-up process that included carefully critiqued rough drafts and a day spent on discussing how to create / insert graphs using GeoGebra and how to structure their writeup in a logical sequence.) Since I am a firm believer that kids learn more through writing about their understanding, the gears in my head are already turning to think about this next modeling assignment.
Anyway, I am VERRRRY excited about this three-variable assignment. Since the topic is already abstract, I kept the patterns linear to make it more accessible to all kids. But, I am very hopeful that it could turn out to be an awesome learning experience.
Addendum: For you new readers, this analogy is what I am going to use to kick off the introduction of 3-variable relationships in the real world.
Saturday, October 20, 2012
It Takes a Village
I have been very gratified by what I consider significant progress this week in some of my students.
Before the October break, I had two students in my "low" Grade 9 class who were refusing to take a test. One of them has Dyscalculia and was simply afraid to try and fail. The other came from a different school, where they had a very difficult time with math, and was afraid of showing the same weakness at the new school. Eventually, after a lot of coaxing and some stern-talking, the kids each sat down to take the test, and they did great!! What an amazing feeling it was for them and me, to get that positive feedback that despite their own tremendous self-doubts, understanding is possible for them. I wish I could take some credit for their success, but the truth is that all the credit goes to them being brave and really, really putting themselves out there by studying for hours for a short test. There is nothing scarier than giving something 100%, and both of them did that and earned the most well-deserved marks in return!!
Then, in Grade 7 I had one child who had done nothing since the beginning of the year, and was falling very behind. Despite my many chats with her, her efforts were minimal and in class she would spend 80 minutes sorting papers or fixing her pen. Outside of class, when I would work with her one-on-one, she would be great, but if there was even a single other kid there, she would stop working entirely. When I set her up with an older student as a tutor, she flaked out twice and the tutor simply gave up on her. Because I was extremely concerned, I had been chatting with the mom over email and in person, and eventually the mom had recommended me to reach out to her elementary school teacher, who had taught her two years ago with some level of success. I reached out to the teacher, talked to the kid, talked to other colleagues to get both the kid and myself out of class in order to meet the elementary teacher (who was only free during a time that we were not free), and we sat down for a three-way conference with the kid. After that, the kid has been a totally different person. She is motivated and progressing rapidly, quickly catching up to the rest of her peers (because she is in fact extremely bright, well above average in terms of her ability to grasp complex material). To encourage her to stay focused, the elementary teacher (who had taught her for 2 years in ES) has offered to support her on the more basic skills for a couple of months until she is completely caught up. I am amazed by my colleague's generosity, and so thankful by the difference it has made in this child to know that she is being looked after and cared for by all the adults in her life.
In the same Grade 7 class I have another child who cannot add or multiply. I reached out to his parents immediately when I discovered that he was having problems, and they said that because he is at a difficult age, we should get him an older boy to act as his mentor / tutor instead of expecting him to always come see me. I found an 11th-grader who has been working with him since, and in my 11th-grader I can see the future of a great math teacher. He is so patient with this kid. The first time he was supposed to meet the 7th-grader, the 7th-grader purposely bailed out on him and stood him up for 30 minutes. Instead of giving up, the 11th-grader dragged me around campus looking for the kid until we found him. This 11th-grade tutor called the kid's parents after the first session and said that the kid needs support at home to work on basic multiplication, and the parents received it well and have been actually doing timed drills with the kid at home. The boy is making slow but sure progress, and my amazing 11th-grader has the goal in mind that by the end of the year, this boy will be on grade level!
One small step at a time. I am trying to reach all kids, and sometimes it is just not possible to do it all myself. It is so gratifying to see when we all pitch in and it makes a difference for one kid. This week, I've been very humbled and thankful and thinking about the phrase that it takes a village to educate a single child.
Before the October break, I had two students in my "low" Grade 9 class who were refusing to take a test. One of them has Dyscalculia and was simply afraid to try and fail. The other came from a different school, where they had a very difficult time with math, and was afraid of showing the same weakness at the new school. Eventually, after a lot of coaxing and some stern-talking, the kids each sat down to take the test, and they did great!! What an amazing feeling it was for them and me, to get that positive feedback that despite their own tremendous self-doubts, understanding is possible for them. I wish I could take some credit for their success, but the truth is that all the credit goes to them being brave and really, really putting themselves out there by studying for hours for a short test. There is nothing scarier than giving something 100%, and both of them did that and earned the most well-deserved marks in return!!
Then, in Grade 7 I had one child who had done nothing since the beginning of the year, and was falling very behind. Despite my many chats with her, her efforts were minimal and in class she would spend 80 minutes sorting papers or fixing her pen. Outside of class, when I would work with her one-on-one, she would be great, but if there was even a single other kid there, she would stop working entirely. When I set her up with an older student as a tutor, she flaked out twice and the tutor simply gave up on her. Because I was extremely concerned, I had been chatting with the mom over email and in person, and eventually the mom had recommended me to reach out to her elementary school teacher, who had taught her two years ago with some level of success. I reached out to the teacher, talked to the kid, talked to other colleagues to get both the kid and myself out of class in order to meet the elementary teacher (who was only free during a time that we were not free), and we sat down for a three-way conference with the kid. After that, the kid has been a totally different person. She is motivated and progressing rapidly, quickly catching up to the rest of her peers (because she is in fact extremely bright, well above average in terms of her ability to grasp complex material). To encourage her to stay focused, the elementary teacher (who had taught her for 2 years in ES) has offered to support her on the more basic skills for a couple of months until she is completely caught up. I am amazed by my colleague's generosity, and so thankful by the difference it has made in this child to know that she is being looked after and cared for by all the adults in her life.
In the same Grade 7 class I have another child who cannot add or multiply. I reached out to his parents immediately when I discovered that he was having problems, and they said that because he is at a difficult age, we should get him an older boy to act as his mentor / tutor instead of expecting him to always come see me. I found an 11th-grader who has been working with him since, and in my 11th-grader I can see the future of a great math teacher. He is so patient with this kid. The first time he was supposed to meet the 7th-grader, the 7th-grader purposely bailed out on him and stood him up for 30 minutes. Instead of giving up, the 11th-grader dragged me around campus looking for the kid until we found him. This 11th-grade tutor called the kid's parents after the first session and said that the kid needs support at home to work on basic multiplication, and the parents received it well and have been actually doing timed drills with the kid at home. The boy is making slow but sure progress, and my amazing 11th-grader has the goal in mind that by the end of the year, this boy will be on grade level!
One small step at a time. I am trying to reach all kids, and sometimes it is just not possible to do it all myself. It is so gratifying to see when we all pitch in and it makes a difference for one kid. This week, I've been very humbled and thankful and thinking about the phrase that it takes a village to educate a single child.
Thursday, August 30, 2012
5-Minute Drills
I am doing daily 5-minute drills this year in grades 7, 8, 11, and 12. It started off with my frustration that kids cannot remember unit circles, even though we had worked on them, explained them, practiced applying them. I was just fed up with them not memorizing the circles. So, instead of feeling frustrated, I decided that during Grade 12 we'd do daily drills of the unit circle at the start of the year. On Day 1, I asked them to take out a piece of scrap paper and to fill out the coordinates of Quadrant I of the unit circle. They failed miserably, so we went over again the hand trick for remembering the coordinates quickly, and I said that at the end of class I'd ask them to do it again. By the end of class, there was much more success (maybe half of the kids were able to get the coordinates correct). I think the immediate feedback helped to motivate them. And then I told them that we'd do the exercise again the next class. And we did, at the beginning and at the end of the next lesson, tagging on to the unit circle basic equations to solve within the range of 0 to 360 degrees. I said that the next time I see them, this'd be a quiz collected for a grade.
In Grade 11 we're doing something similar, but primarily to review older prerequisite skills (such as writing line equations) that I think the kids should already know, and that I only wish to brush up on. We would do the same skill at the start of class, end of class, and next start of class. And then soon we'd have a mini quiz on it also at the start of a class, collected for a grade.
So, a long time ago when I taught middle school for the first time, our school implemented daily quizzes. I kind of hated them, because it was so much grading, even though it was a good practice for the kids. I really like my new 5-minute drills, because I think they are the best of both worlds. The kids still feel the time pressure and the need to be correct, but they're not graded that often and it's less work for me. For my Grade 7 and Grade 8 students, I let them do two problems a day on mini whiteboards. (I got lucky and was gifted a class set, along with markers and erasers, when I sent out a request asking to borrow them.) This is important because in Grades 7 and 8 we are working on basic skills like fractions, percents, equations, etc. The boards are a nice way to quickly check in with all kids on a daily basis, and I can see who is sure of themselves and who is not. Now that I have taught with mini whiteboards, I really don't think I can go back! I love that kids also write their normally snarky comments on the whiteboards instead of calling them out, so that only I can "hear" those comments. Cuteness. I saw one kid write "DUH!" on his board when another kid made an obvious observation. One day I kept them over the class accidentally (since our school does not have bells), and a kid raised his board that said, "Class ended!" So, they're great for classroom management as well as daily assessment.
I'm still trying all kinds of things this year, but working close to 60 hours this week is taking its toll. Grade 9 is my baby, because this again is a very low class, and this year a bigger group. I will be doing all kinds of experimental things with them, and if it works, I'll share the strategies with y'all. So far, so good. The kids are able to graph linear functions by making tables, and they're able to write linear equations from a table. Not a bad first week for kids who couldn't graph points on Day 1!!! They also go around and check off each other's answers, which I think is so awesome because they need to be building confidence alongside content knowledge.
So, 60 hours-ish this week. A bit rough. But I am loving it!!! I also really love sharing classrooms this year. I teach in about 5 different rooms, and I just love it. Even though I have to carry my supplies everywhere and it's a pain, I am all in other people's spaces and talking to them regularly as a result. It's really nice, because it forces me out of being in the workaholic zone. Anyway, I am hoping that things will calm down soon on the department chair side, so that I can get back to a normal work schedule and re-gain work-life balance.
I hope your years are off to a wonderful start! :) Hi web, goodbye web. See you soon, hopefully.
In Grade 11 we're doing something similar, but primarily to review older prerequisite skills (such as writing line equations) that I think the kids should already know, and that I only wish to brush up on. We would do the same skill at the start of class, end of class, and next start of class. And then soon we'd have a mini quiz on it also at the start of a class, collected for a grade.
So, a long time ago when I taught middle school for the first time, our school implemented daily quizzes. I kind of hated them, because it was so much grading, even though it was a good practice for the kids. I really like my new 5-minute drills, because I think they are the best of both worlds. The kids still feel the time pressure and the need to be correct, but they're not graded that often and it's less work for me. For my Grade 7 and Grade 8 students, I let them do two problems a day on mini whiteboards. (I got lucky and was gifted a class set, along with markers and erasers, when I sent out a request asking to borrow them.) This is important because in Grades 7 and 8 we are working on basic skills like fractions, percents, equations, etc. The boards are a nice way to quickly check in with all kids on a daily basis, and I can see who is sure of themselves and who is not. Now that I have taught with mini whiteboards, I really don't think I can go back! I love that kids also write their normally snarky comments on the whiteboards instead of calling them out, so that only I can "hear" those comments. Cuteness. I saw one kid write "DUH!" on his board when another kid made an obvious observation. One day I kept them over the class accidentally (since our school does not have bells), and a kid raised his board that said, "Class ended!" So, they're great for classroom management as well as daily assessment.
I'm still trying all kinds of things this year, but working close to 60 hours this week is taking its toll. Grade 9 is my baby, because this again is a very low class, and this year a bigger group. I will be doing all kinds of experimental things with them, and if it works, I'll share the strategies with y'all. So far, so good. The kids are able to graph linear functions by making tables, and they're able to write linear equations from a table. Not a bad first week for kids who couldn't graph points on Day 1!!! They also go around and check off each other's answers, which I think is so awesome because they need to be building confidence alongside content knowledge.
So, 60 hours-ish this week. A bit rough. But I am loving it!!! I also really love sharing classrooms this year. I teach in about 5 different rooms, and I just love it. Even though I have to carry my supplies everywhere and it's a pain, I am all in other people's spaces and talking to them regularly as a result. It's really nice, because it forces me out of being in the workaholic zone. Anyway, I am hoping that things will calm down soon on the department chair side, so that I can get back to a normal work schedule and re-gain work-life balance.
I hope your years are off to a wonderful start! :) Hi web, goodbye web. See you soon, hopefully.
Thursday, May 24, 2012
Completing the Square Geometrically
I am so excited! I taught completing the square today in my "low" grade 9 class for the first time, and I decided to try a geometric approach this time as inspired by my friend from PCMI (the awesome Danielle Soderberg*), and the kids loved it!! After just two examples on the board, they had no trouble at all working through cases with integer leading coefficients and integer vertices. It was fantastic.
Here was the worksheet I made for completing the square, and here was the warmup sheet I used prior to introducing complete the square (cut into half-sheet strips; the kids skipped the conversion to vertex form at the beginning of class and came back to that column at the end, after the lesson).
Enjoy!
*Although, as a small disclaimer, I never saw Danielle's worksheets, so it's quite possible her approach is different and/or it is far superior. She vaguely mentioned something about algebra tiles and completing the square.
Here was the worksheet I made for completing the square, and here was the warmup sheet I used prior to introducing complete the square (cut into half-sheet strips; the kids skipped the conversion to vertex form at the beginning of class and came back to that column at the end, after the lesson).
Enjoy!
*Although, as a small disclaimer, I never saw Danielle's worksheets, so it's quite possible her approach is different and/or it is far superior. She vaguely mentioned something about algebra tiles and completing the square.
Monday, March 26, 2012
Functions Fun with 9th-Graders
I have to say that as a classroom orchestrator, my weakness is in setting up DRAMA in my lessons. I do, however, put on a great big show every year if there is a group of kids to whom I have to introduce functions for the first time. I do a big show of function machines (not a unique idea, obviously), by gradually feeding input numbers written on post-its into a "Function Machine" (this year, it was a black plastic bag with a "Function Machine" label on it) and flipping the post-it over inside so that the kids can be delighted by the output value that comes out. You might think the kids are too old for this, but NO! This year, one of my Grade 9 boys had to stifle a giggle when the first number transformed inside the function machine. His eyes got so big. Together, as a class, we fill out a function diagram on the board ONE post-it at a time (and the kids copy it down in their notes), so that they can see how the function diagram visually represents the mapping of the elements. At some point they start to feel very antsy to make predictions for the next outputs once they start to see a pattern between input-output pairs, so that sense of anticipation really teaches them about the predictability nature of functions. At some point, when they absolutely cannot stand how smart they are anymore, I ask, "So, if we put in some number x as the input, what will be returned?" And when they give me the answer, I both write x ----> x + 2 (for example) as a pair inside the function diagram, and underneath I write in a parallel formal notation:
f(x) = x + 2
And at that moment, with a tiny bit of clarification, it becomes crystal clear to them what each part of the function notation represents. (Obviously, it still takes practice to gain confidence/familiarity with the notation, but I think putting it directly underneath the x ----> x + 2 notation definitely helps to clarify why there is an X on the left side of the equal sign.)
Then, we repeat several other dramatic sequences (with increasingly complex patterns), each time referring firmly back to the definition on the board of a function HELPING US MAKE PREDICTIONS; each X value has exactly 1 Y value. I try to vary up the representations for the later examples, using tables or ordered pairs, so they can realize that all representations are actually equivalent. (Towards the end, to help them focus their understanding, obviously we look at cases of both shared outputs AND two outputs for same input, and we use our function definition of PREDICTABILITY to try to evaluate which case is a function and which is not.)
There are other things I do on Day 1 of functions that I think also help to clarify the definition of a function (such as a sorting activity involving cards that have maybe-functions printed on them), but the DRAMA! is what is so fun about this particular lesson introduction. I absolutely love it every year, even though it's so simple in nature and in foresight always seems potentially very cheesy. --And, trust me, I know that if my 9th-graders are glued to my every move at the board, it's a lesson to keep for the long haul. :)
Do you have your own favorite dramatic introductions of new concepts??
f(x) = x + 2
And at that moment, with a tiny bit of clarification, it becomes crystal clear to them what each part of the function notation represents. (Obviously, it still takes practice to gain confidence/familiarity with the notation, but I think putting it directly underneath the x ----> x + 2 notation definitely helps to clarify why there is an X on the left side of the equal sign.)
Then, we repeat several other dramatic sequences (with increasingly complex patterns), each time referring firmly back to the definition on the board of a function HELPING US MAKE PREDICTIONS; each X value has exactly 1 Y value. I try to vary up the representations for the later examples, using tables or ordered pairs, so they can realize that all representations are actually equivalent. (Towards the end, to help them focus their understanding, obviously we look at cases of both shared outputs AND two outputs for same input, and we use our function definition of PREDICTABILITY to try to evaluate which case is a function and which is not.)
There are other things I do on Day 1 of functions that I think also help to clarify the definition of a function (such as a sorting activity involving cards that have maybe-functions printed on them), but the DRAMA! is what is so fun about this particular lesson introduction. I absolutely love it every year, even though it's so simple in nature and in foresight always seems potentially very cheesy. --And, trust me, I know that if my 9th-graders are glued to my every move at the board, it's a lesson to keep for the long haul. :)
Do you have your own favorite dramatic introductions of new concepts??
Saturday, March 17, 2012
My So-Called Remedial Class
I've been teaching a "remedial" Grade 9 class this year. It is actually my first time teaching an actual remedial class! In all the other years of teaching, either I taught heterogeneous classes (sometimes with very weak students mixed in), or I taught classes that were meant to be mainstream or even honors classes within a streamed setting.
I am teaching a "remedial" Grade 9 class. In the beginning, it was very rocky. In between me being a new teacher at the school and the kids being sorted by levels for the first time in their lives, there was a lot of upheaval and a lot of unhappy kids and parents. In the end, I ended up with 10 students (in my smallish classroom). They were very weak and all the boys could not sit still and they refused to speak English in the classroom. (I've dealt with very severe ADHD at my last school, with kids falling out of their seats and 5 ADHD kids in a class of 20, so hyperactivity is not really a problem for me.) And they were rude to me out of anger about the situation, so they made snide German comments to each other daily. They wanted an expressway to a "normal" class and they did not believe me when I said that I would be teaching them normal grade 9 material, but in a different way that allows them to cover more ground in a year in order to catch up. There was a lot of hurt and a lot of anger/resentment, so the class was an uphill battle from the start.
Well, fast forward to now. It's March. I just gave a pretty hard trigonometry test to these same "remedial" class kids. On this test, almost every problem was a word problem, for which they would have to draw their own diagrams before even getting to the solving part. It involved a lot of thinking. --AND THEY DID GREAT!!! Generally speaking, they have been doing good work for me this year, and it's more and more apparent to me that the boys in the class simply needed a different way of teaching that fit their active personalities. Maybe what they had needed was a teacher from the Bronx who would give things to them straight. But, whatever it is, these kids are WORKING, and even a boy who had never bothered to do any math in his entire life up until January, has been trying very hard and got a majority of the questions on the previous trig quiz, correct. Even though they were all multi-stepped!! It took him twice as long as everyone else to do that, obviously, because I think it was the first time in his life that he actually sat down to try to gather his thoughts and to REALLY try every problem on an exam after having worked in class for 2 weeks straight.
I feel so positive about this. One of the boys had gotten perfect scores on two consecutive quizzes, so now there is even a level of healthy competition going on amongst friends.
I am still trying to figure out what the deal is with my girls, however. My boys, I think I've got a handle on. My girls who work consistently, on the other hand, are not always able to show that off on the test. (I was able to promote two girls to the mainstream class at the semester, so obviously this statement does not pertain to all my girls. But, I got another girl in exchange who was moved down from the mainstream class...) So, the work is still cut out for me, but I most definitely look forward to this class more and more, and I am excited that I will get to keep teaching them through next year, now that I have an actual relationship with each of them that I am building on top of. (They have since stopped being rude to me. Well, most of the time anyway. They don't call out, they raise their hands to explain stuff, they listen to each other most of the time... Many of them even do weekly homework, 20 problems of their choice from the textbook!!)
PS. You can see a copy of my said trig test here. Sorry but the font is small -- for two reasons: one is that I am almost out of printing quota for the month. The other is that I created this on a Mac instead of my normal PC, and so I had to send it to myself as a PDF and couldn't modify it afterwards. Doh.
But see? If you look at this test, I don't think you (nor I) would expect half of a "remedial" Grade 9 class to have aced this. It is true: 3 out of 9 kids missed nearly nothing (only rounding errors and such), and 2 more made only very minor calculator-entry errors. That is not bad!
I am teaching a "remedial" Grade 9 class. In the beginning, it was very rocky. In between me being a new teacher at the school and the kids being sorted by levels for the first time in their lives, there was a lot of upheaval and a lot of unhappy kids and parents. In the end, I ended up with 10 students (in my smallish classroom). They were very weak and all the boys could not sit still and they refused to speak English in the classroom. (I've dealt with very severe ADHD at my last school, with kids falling out of their seats and 5 ADHD kids in a class of 20, so hyperactivity is not really a problem for me.) And they were rude to me out of anger about the situation, so they made snide German comments to each other daily. They wanted an expressway to a "normal" class and they did not believe me when I said that I would be teaching them normal grade 9 material, but in a different way that allows them to cover more ground in a year in order to catch up. There was a lot of hurt and a lot of anger/resentment, so the class was an uphill battle from the start.
Well, fast forward to now. It's March. I just gave a pretty hard trigonometry test to these same "remedial" class kids. On this test, almost every problem was a word problem, for which they would have to draw their own diagrams before even getting to the solving part. It involved a lot of thinking. --AND THEY DID GREAT!!! Generally speaking, they have been doing good work for me this year, and it's more and more apparent to me that the boys in the class simply needed a different way of teaching that fit their active personalities. Maybe what they had needed was a teacher from the Bronx who would give things to them straight. But, whatever it is, these kids are WORKING, and even a boy who had never bothered to do any math in his entire life up until January, has been trying very hard and got a majority of the questions on the previous trig quiz, correct. Even though they were all multi-stepped!! It took him twice as long as everyone else to do that, obviously, because I think it was the first time in his life that he actually sat down to try to gather his thoughts and to REALLY try every problem on an exam after having worked in class for 2 weeks straight.
I feel so positive about this. One of the boys had gotten perfect scores on two consecutive quizzes, so now there is even a level of healthy competition going on amongst friends.
I am still trying to figure out what the deal is with my girls, however. My boys, I think I've got a handle on. My girls who work consistently, on the other hand, are not always able to show that off on the test. (I was able to promote two girls to the mainstream class at the semester, so obviously this statement does not pertain to all my girls. But, I got another girl in exchange who was moved down from the mainstream class...) So, the work is still cut out for me, but I most definitely look forward to this class more and more, and I am excited that I will get to keep teaching them through next year, now that I have an actual relationship with each of them that I am building on top of. (They have since stopped being rude to me. Well, most of the time anyway. They don't call out, they raise their hands to explain stuff, they listen to each other most of the time... Many of them even do weekly homework, 20 problems of their choice from the textbook!!)
PS. You can see a copy of my said trig test here. Sorry but the font is small -- for two reasons: one is that I am almost out of printing quota for the month. The other is that I created this on a Mac instead of my normal PC, and so I had to send it to myself as a PDF and couldn't modify it afterwards. Doh.
But see? If you look at this test, I don't think you (nor I) would expect half of a "remedial" Grade 9 class to have aced this. It is true: 3 out of 9 kids missed nearly nothing (only rounding errors and such), and 2 more made only very minor calculator-entry errors. That is not bad!
Saturday, March 3, 2012
Going Sloooooooow on Exponent Rules
One thing that always troubles me is that many students tend to want to rush to draw procedural generalizations before they reach a solid conceptual understanding. What this means is that in two weeks, when I'm not standing in front of them, they do not remember how to properly apply the rules and cannot even retrieve the relevant concepts to re-engineer those rules! argh.
This year, for teaching exponents, I am going to sloooooooow them down to try to avoid that.
Here is my attempt at pulling together a worksheet on exponents (which, granted, isn't the most exciting of topics). Check it out - I like this worksheet and think it will work pretty well, even though everything in it looks very basic. We need to build sloooow conceptual understanding, and after that we will drill the rules using some games!




Addendum March 14, 2012: This lesson (parts 1 and 2) worked like a charm today!! I am feeling extremely positive about the outcome. The students could explain to me with NO PROBS WHATSOEVER why when you add or subtract terms with exponents, the resulting exponents don't change, but when you multiply them, they do change. My faster students were finished with the entire worksheet and did not have any misunderstanding at the end. They're ready for Phase 2: simplification drill games!!
This year, for teaching exponents, I am going to sloooooooow them down to try to avoid that.
Here is my attempt at pulling together a worksheet on exponents (which, granted, isn't the most exciting of topics). Check it out - I like this worksheet and think it will work pretty well, even though everything in it looks very basic. We need to build sloooow conceptual understanding, and after that we will drill the rules using some games!




Addendum March 14, 2012: This lesson (parts 1 and 2) worked like a charm today!! I am feeling extremely positive about the outcome. The students could explain to me with NO PROBS WHATSOEVER why when you add or subtract terms with exponents, the resulting exponents don't change, but when you multiply them, they do change. My faster students were finished with the entire worksheet and did not have any misunderstanding at the end. They're ready for Phase 2: simplification drill games!!
Subscribe to:
Posts (Atom)